задание 15 (неравенство)

Уравнения и неравенства

[block]((x^2 + 9x + 20) * log(x + 6) (x + 5) * lg(x + 2)^2)/(2*x^2 + 21x + 54) меньше или равно 0[/block]

(8^(x+1)-40)/(2*64^x-32) меньше или равно 1

log(16)(x+5) + log(x^2+10x+25) 2 ≥ 3/4

(4x - 7)*log(x^2-4x+5)(3x - 5) ≥ 0

[m]
\frac{log_{2x-1}^{2}(9x^{2}-12x+4) - 10log_{2x-1}(3x-2)+18}{3log_{2x-1}(6x^{2}-7x+2)-2} \leq 2.
[/m]

[block](sqrt(2x^2 + 5x - 18))/(log(0,5) |x + 5|)≥ 0[/block]

log3 3/x * log5 x + log5 45 * log3 x > 1 + 2log5 3

[block](2^(4x) - 2^(3x+1) + 2^(2x+1) - 2^(x+1) + 1)/((2^(x) - 2)^3 + (2^(x) - 3)^3 - 1) больше или равно 0[/block]

[m]
\frac{4^{\sqrt{x-1}} - 5 \cdot 2^{\sqrt{x-1}} + 4}{\log_{2}^2 (7 - x)} \geq 0.
[/m]

[m]
\frac{(2^x - 2)^3}{2^{x+2} - 12} \geq \frac{8^x - 4^{x+1} + 2^{x+2}}{9 - 4^x}
[/m]

log(1/5)(x-10)-log(1/5)(x+2) больше или равно -1

log^2_(x) (x + 2) ≤ log^2_(x+2) x.

3^(tg(x^2 - 1)) ≥ (x + 1)^(tg 3)

[block](25^x - 5^(x+2) + 26)/(5^x - 1) + (25^x - 7 · 5^x + 1)/(5^x - 7) ≤ 2 · 5^x - 24[/block]

[block](x^3 + 3x^2 + 3x + 3)/(x^2 + 3x) больше или равно x + (1)/(x+2) + (1)/(x)[/block]

[block](2^x)/(2^x-3) + (2^x+1)/(2^x-2) + (5)/(4^x-5*2^x+6) меньше или равно 0[/block]

log3(x^2+2)-log3(x^2-x+12) больше или равно log3(1 - 1/x)

9^(log6x) + 2x^(log6 9) < 3*x^(2log2 3)

[block]((3^x - 3)^3)/(2 * 3^x - 4) ≤ (27^x - 2 * 3^(2x+1) + 3^(x+2))/(3^x - 9^x + 2)[/block]

[block]((2^x - 8)(lg x - 1))/((log(1/2) x + 1)(sqrt(12 - x))) > 0[/block]

log3 ( (1/х) - 3) + log3 ( (1/х) + 3) ≤ log3 (64х - 9)

Решите неравенство [m]\frac{3^{(x^2 - 1)\log_{\sqrt{3}} 16} - 32^{x - 1}}{1 - 2x} \leq 0[/m].

log₂(x+1) + log₃(x) ≤ 3

x^2 · log(81) x ≥ log(81) x^5 + x · log3 x

log(x/3) log(x) sqrt(3 − x) ≥ 0

Решите неравенство:
[m]\frac{(x^2 + x) \log_8(x^2 + 4x - 4)}{|x - 2|} \geq \frac{\log_8 (-x^2 - 4x + 4)^6}{x - 2}.[/m]

1/cos²x - 3/sin((11π/2)-x) = -2

[-2π, -π/2]

Решите неравенство.

log₂(17x² + 16) - log₂(x² + x + 1) ≥ log₂(x / (x + 10) + 16)

Решите неравенство

log(1/3) (3x - 1) / (x + 2) < 1

log7(5x^2-4)-log7x < log7(5x^2 + 1/x - 5)

Решить неравенство log(x-3) (x^2 - 2x + 1) <= 1;

[block](3^(x^2 + x) - 4 * sqrt(3)^(x^2 + x) + 3)/(sqrt(x) - sqrt(x + 4)) ≤ 0[/block]

Решить неравенство 5 log6 (x^2 + x - 12) ≤ 12 + log6 ((x - 3)^5 / (x + 4))

Решите неравенство log_(2x+4)(x^(2)-3x+10) ≥ 1

Решить неравенство
[m]\frac{\log_3 x}{\log_3 \left(\frac{x}{81}\right)} + \frac{3}{\log_3 x} + \frac{8}{\log_3^2 x - \log_3 x^4} \geq 0 [/m]

Решите неравенство

log(12)(x - 3) - log(x-2)(x - 5) + 1/log(x-5)12 ≥ log(x-2)(x - 3).

Решите неравенство:

[block](log5 (25x^2) + 48)/(log^2_5 x - 49) >= -1[/block]

Решите неравенство:
[block](2^x)/(2^x - 16) + (2^x + 16)/(2^x - 4) + (258)/(4^x - 20 * 2^x + 64) ≤ 0[/block]

Решите неравенство log^2_x (x-2) ≤ log^2_(x-2) x

Решить неравенство

|x^2 - (29/12)x - 35/12| ≥ 2x^2 - (61/12)x - 19/12

Решить неравенство

[block](4^(x^2 - 2x) - 16 · 2^((x - 1)^2) + 35)/(1 - 2^((x - 1)^2)) ≤ 4^x · 2^((x - 2)^2)[/block]

Решить неравенство

[block](30 * 5^(x+3) - 0.2^(x+1))/(5^(3-x) - 25^(1-x)) ≥ 5^(x-3)[/block]

Решить неравенство
[block](x + (3)/(x)) * ((sqrt(x^2 - 6x + 9) - 1)/(sqrt(5 - x) - 1))^2 ≥ 4 * ((sqrt(x^2 - 6x + 9) - 1)/(sqrt(5 - x) - 1))^2[/block]

Решите неравенство 9^x + 54/x^2 ≥ 7*(3^(x+1))/x.

Решить неравенство log5((3-x)(x^2+2)) ≥ log5(x^2-7x+12) + log5(5-x)

Решите неравенство log(|x-6|)(7 - |x|) ≤ 1.

Решить неравенство
[block](9^x-3^x+2)/(9^x-3^x)+(5*3^x-19)/(3^x-4) ⩽ (2*3^(x+1)-2)/(3^x)[/block]

Решить неравенство
[block](10^x-25*2^x-2*5^x+50)/(5x-x^2-4) ≥ 0[/block]

Решить неравенство log5(64x^2-9)-log5(x) ≤ log5(65x+(21/x)-11)

Решите неравенство
[block]log((x-2)^2) (5-x)/(4-x) ≤ 1 + log((x-2)^2) (1)/(x^2 - 9x + 20)[/block]

Решите неравенство log^2_(0,5) x - 4log(0,5) x + 3 > 0

Решите неравенство
[block](4x^4 - 4x^3 + x^2)/(-2x^2 + 5x - 2) + (2x^3 - 7x^2 + 5x + 1)/(x - 2) ≤ 0[/block]

Решите неравенство -8|x^2-1|-2 ≥ 1/(x^2-1)

Решить неравенство log(x-1)(-x^2+8x-7) - (1/16)log(2x-1)(x-7)^2 ≥ 2

Решить неравенство
[block](log_5 (x^2 - 2x))/(log_5 x^4) ≥ 0,25[/block]

Решите неравенство
[block](x-8x+11)/(x-6) + (x^2-9x+2)/(x-9) <= 2x-2 [/block]

5^(x+3) - 5^(x+2) - 5^x < 6^(x/2 + 3) - 6^(x/2 + 2) + 3 * 6^(x/2 + 1).

Решите неравенство log^2_7(x + 5) ≥ log_7(x - 2) ⋅ log_(x - 2)(x + 5).

Решите неравенство
[block](log^2_(x-2) (6-x))/(x^2-10x-24) >= 0[/block]

Решить неравенство 2log2(1-2x) - log2((1/x) - 2) ≤ log2(4x^2 + 6x - 1)

Решите неравенство log(81x) 9 ∙ log^2_(1/3) (27x) ≤ 4.5

Решите неравенство: log(2x+2)(2x - 5)^2 ≤ 2log(2x+2)(x + 1)

Решить неравенство [m] \frac{\log_{5}(x^2 - 12x + 36)}{\log_{5}(x - 1)} \le 0 [/m]

Решить неравенство 8log4sqrt(x) + log2(x + 8/x^2) ≤ 2 log2((x^2 + 2x)/2)

Решите неравенство
[block](log_3 (9x) - 13)/(log^2_3 x + log_3 x^4) ≤ 1[/block]

Решить нервество log(sqrt(3))log(sqrt(2))( x - log₅ 6) < 0

Решите неравенство 2·sqrt((2x−1)^2) + sqrt(x^3 + x^2−4x−4) ≤ 2−4x.

log₂(x-1) + log₂(x² + 1/(x-1)) ≤ 2log₂((x² + x - 1)/2)

Решить неравенство (1 / log(2^x-1)2) * log(√2)(4^(x+1) - 2^(x+3) + 4) < 80

Решить неравенство log(0,5)(5^(1 + lg x) - 0,5^(1 + lg x)) ≤ lg x - 1

Решить неравенство 9^x - 2^((2x+1)/2) < 2^((2x+7)/2) - 3^(2x-1)

Решить неравенство log₂ (4x²-1) - log₂ x ≤ log₂ (5x + 9/x -11)

Решите неравенство log^2_3|x| - log3(x^2/3) ≥ ( (1/3) log3(27|x|) )^2

а) Решите уравнение 2cos^2(5Pi/2 + x) + sqrt(2)sinx = 0

б) Укажите его корни, принадлежащие отрезку [9Pi/2; 6π].

Решить неравенство log2(x-1)+log2(x^2+1/(x-1)) ≤ 2log2((x^2+x-1)/2)

Решите неравенство log((x-2)^2) (5-x)/(4-x) ≤ 1 + log((x-2)^2 ) 1/(x^2 - 9x + 20).

Решите неравенство: log5x + log(x)x/3 < (log5x(2 - log3x)) / log3x

Решите неравенство [m]log_{0.5}^{2}(4x) · log_{0.25}(0.25x)^{2} <= log_{0.5}5 · log_{5}(x/4).[/m]

Решить неравенство log(1/81)(36-5x)*log(8-x)1/9 >= 1

Решите неравенство sqrt(1-log2x) ((x-3)(x+5))/(x+1) >= 0

Решить неравенство
[block](3^(x+1))/(3*2^x-2*3^x)-(3^x)/(2^x-3^x) >= 0[/block]

Решите неравенство (1/8)log2(x - 2)^8 + log2(x + 4) ≥ 3.

Решите неравенство log^2_5 |x| - log5(x^2/5) >= ((1/2)log5 (25|x|))^2

Решить неравенство sqrt(2+log(1/5)(x))*((x-15)(x-27))/(x-30)) ≤ 0

Решить неравенство
log(15)(x+5) + log(15)(x^2 + 1/(x+5)) ≤ 2log(15)(x^2 + x + 5)/2

Решите неравенство

log3(x+7)+(1/6)log3(x+1)^6 ≥ 2

Решить неравенство x^2*log(625)(3-x) ≤ log5(x^2-6x+9)

Решить логарифмическое неравенство
log(25)(5^x-1)*log5(5^(x+2)-25) < 4

Решите неравенство

[block]log2((7^(-x^2)-6)(7^(-x^2+9)-1)) + log2 (7^(-x^2)-6)/(7^(-x^2+9)-1) > log2(7^(3-x^2)-5)^2[/block]

Решите неравенство (x^2 + 2x - 3)*log(1+cos x)(9 + 2x - x^2) ≥ 0

Решите неравенство log2(x-4) - 3log2((x+2)/(x-2)) > 2

Решить неравенство log^2_4 (2x) + log(1/2) sqrt(x)/2 > 1,5

Решите неравенство 36^x-2*18^x >= 8*9^x

Решить неравенство:

3log4(x^2+5x+6) ≤ 5 + log4((x+2)^3/(x+3))

Решите неравенство:

log(x+2) (7x^2 + 11x - 6) < 2

Решить систему уравнений

{ 5^(log5(x-y)) = 1
{ 3^x-3^(y) = 6log2 8

Решить неравенство

|x^3 - 2x^2 + 2| ≥ 2 - 3x

Решить неравенства

[block](log2 x)/(log2 (4x + 7)) ≤ 1[/block]

Решить неравенства

[block](log2 (4x+3) * log5 (2x+5))/(log3 (6x) * log4 x) ≥ 0[/block]

Решите неравенство
[block](log_(x+3)(x^2 - x + 30))/(log_(x+3)(x^2 - x - 1)) ≥ (lg(x^4 - 2x^2 + x^2))/(lg(x^2 - x - 1))[/block]

Решить неравенство |x—3|^(2x^2-7x) > 1.

2^(log8(x^2-6x+9)) ≤ 3^(2log(x)sqrt(x)-1)

Решите неравенство

(2^x + 3*2^(-x))^(2log2x-log2(x+6)) > 1

Решите неравенство

(2x+1)log5 10 + log5(4^x - 1/10) ≤ 2x-1

Решить неравенство
[m](x-4)(\log_{5}{(125-25x)}-\log_{6}{(x^2+x-6)}+\frac{1}{\log_{(5-x)}{0,2}}+x+6) ≤ x^2+2x-24[/m]

Решить неравенство
(x^2-7x+12)*log(x-2)(x-3)*ln(x-6)^2 / 2x^2-11x+14 ≤ 0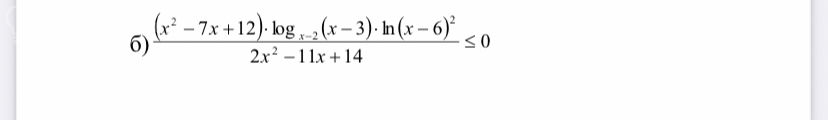

Решить неравенство log3 (1/x) + log3 (x^2+3x-9) ≤ log3(x^2+3x+(1/x)-10)

Решить неравенство

[block](log4(2-x)-log_(14)(2-x))/(log_(14)x-log(49)x) ≤ log4 49[/block]

lgx+lg(x-10) < lg6

log(15)(x^2-4x+3) < 1

Решить неравенство log4(7x+4)-log4(2x-1) < 1

Решите неравенство [m]5^{log^2_{5}x}+x^{log_{5}x} ≥ 2\sqrt[4]{5}[/m]

Решите неравенство

sqrt(x+(2/3))(log2log(1/2)|1+x|) ≤ 0

Решите неравенство: (x-7)log(x+5)(7-2x) ≥ 0

Решите неравенство

log5(x+2)^2*log(1/2)x^2 - 4log5(x+2) + 4log2(-x) + 4 ≤ 0

Решите неравенство

log^2_3(-log3x) + log3log^2_3x ≤ 3

Решить неравенство

[block](sqrt(4x-x^2-3))/(x+5) меньше или равно (sqrt(4x-x^2-3))/(2x+3)[/block]

Решить неравенство [m](\frac{1}{10})^{\frac{x-3}{x+1}}\geq 10^{-\frac{3}{x+1}}[/m]

Решите неравенство

[block]log(|x+3|) (2x+6)/(|x|) ≤ 1[/block]

Решите неравенство

[block](1+sqrt(6+5x-4x^2))/(log(3x+3)7) ≥ 0[/block]

Решите неравенство

[block](6)/(3-sqrt(log2(x+12))) больше или равно 2+sqrt(log2(x+12))[/block]

Решить неравенство

[m]\frac{1}{\log_6(7-5x^2)}+2 = \log_{7-5x^2}(49-25x^4)[/m]

Решить неравенство

27*45^x - 27^(x+1) - 12*15^x + 12*9^x + 5^x - 3^x ≤ 0

Решите неравенство

log(11)(8x^2+7)-log(11)(x^2+x+1) больше или равно log(11)((x/(x+5))+7)

[m]1+\frac{10}{(\log_2x)-5} + \frac{16}{\log^2_2x-\log_2(32x^5)+5} ≥ 0[/m]

Решить неравенство

Решите неравенство logx 3 + 2log3x 3 - 6log9x 3<=0

Решить неравенство

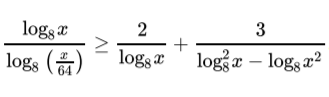
[block](2*3^(2x+1) - 7*6^x + 2*4^x)/(3*9^x-3^x*2^(x+1)) ≤ 1[/block]

Решить неравенство 2x ≥ log2((35/3)*6^(x-1)-2*9^(x-1/2))

Решить неравенство sqrt(log3x)+2sqrt(log(x)3) ≥ 3

Решите неравенство
[block](log2(4x^2)+35)/(log^2_2x - 36) ≥ -1[/block]

( 3*25^x+0,5 )+4^2x+1,5 <= 22*20^x реши неравенство

Решить неравенство
[block](log(x)(2x^(-1))*log(x)(2x^2))/(log(2x)x*log(2x^(-2))x) < 40[/block]

Решите неравенство

[block](4^x-2^(x+3)+7)/(4^x-5*2^x+4) ≤ (2^x-9)/(2^x-4) + (1)/(2^x-6)[/block]

Решите неравенство log(x)(x-2)*log(x)(x+2) ≤ 0

Решить неравенство

[m]3^x+\frac{2*3^{x+1}}{3^x-3}+\frac{9^x+26*3^x+21}{9^x-4*3^{x+1}+27} ≤ 1[/m]

Решить неравенство

[m]\log^2_5 \frac{(x-4)^2(x-3)}{48} > \log^2_{0,2} \frac{x-3}{3}[/m]

Решите неравенство

[m]125^x-25^x+\frac{4*25^x-20}{5^x-5} ≤ 4[/m]

Решите неравенство [m]2^{\frac{x}{x+1}} - 2^{\frac{5x+3}{x+1}} + 8\leq 2^{\frac{2x}{x+1}}[/m]

Решить неравенство

[block]((x^2+9x+20)*log(x+6)(x+5)*lg(x+2)^2)/(2x^2+21x+54) ≤ 0[/block]

Решите неравенство log(x-2)(3x-x^2) ≤ 2

Решите неравенство [m]\log_{0,25x^2} \frac{x+6}{4} \leq 1[/m]

Решите неравенство

log(10-x^2)([m]\frac{16}{5}[/m]x-x^2) < 1

Решить неравенство

[m]\frac{2\log_5(x^2-5x)}{\log_5x^2} \leq 1[/m]

Решите неравенство

[m]\frac{(x^2-x-14)^2}{2x+\sqrt{21}} \leq \frac{(2x^2+x-13)^2}{2x+\sqrt{21}} [/m]

Решить неравенство

log2(x-1)(x^2+2) ≤ 1+log2(x^2+3x-4) - log2x

log2(x-1)(x^2+2) ≤ 1+log2(x^2+3x-4)-log2x

Решить неравенство

(2-3x)log(2x-1)(x^2-2x+2) ≤ 0

Решить неравенство

[m]\frac{lg(3x^2-3x+7)-lg(6+x-x^2)}{(10x-7)(10x-3)} \geq 0[/m]

Решите неравенство

[block]3^(x^2-4x-5)+log3 (x - 3)/(6) меньше или равно 0[/block]

Решите неравенство

log(x+1)(x-1)*log(x+1)(x+2) ≤ 0

Решить неравенство:

Решить неравенство

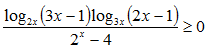
log4(6-6x) < log4(x^2-5x+4) + log4(x+3)

Решить неравенство log2(4-4x) ≥ log2(x^2-4x+3)-log2(x+2)

Решить неравенство

log3(x^2-x-3)+log3(2x^2+x-3) ≥ log3(x^2-2)^2+2+log(1/3)4

Решить неравенство 3^(x^2)*5^(x-1) ≥ 3

Решить неравенство (log2(x+5))/(2^(x+2)-4^x-3) меньше или равно log2(x+5)

Решить неравенство log(-1-x)((-4-x)/(x+1)) ≤ -1

2log9(4x^2+1) ≥ log3(3x^2+4x+1)

log_(1/3)(-x)>log_(1/3)(4-2x)

log3(4-4x) ≥ log3(x^2 - 4x + 3) + log3(x+2)

Решить неравенство sqrt(x-4)(5^(x-3)+6^(x-2)-40) меньше или равно 0

Решить неравенство log(1/4)(48-16x)>log(1/4)(x^2-8x+15)+log(1/4)(x+3)

log(0,1) (6-6x) ≤ log(0,1) (x^2-4x+3) + log(0,1) (x+4)

log6 (21-7x) больше или равно log6 (x^2-8x+15)×log6 (x+3)

log5 (25-25x) > log5 (x^2-4x-3)+ log5 (x+7)

Решите неравенство

log(1/10)(6-6x) ≥ log(1/10)(x^2-4x+3) + log(1/10)(x+4)

1) log_(sqrt(3))(2x-3)<4

3) log_(1/2)(6-x) ≥ log_(1/2)x^(2)

Решите неравенство: log(x+2)(2x^2-x-1) ≤ log(x-1)(x^2+2x+3) / log(x-1)(x+2)

log_(0,6)(18-18x) ≤ log_(0,6)(x^(2)-6x+5)+log_(0,6)(x+4)

Решите неравенство

(1/3)^((7x-x^2-9)/x) - 4*(1/15)^((7x-x^2-9)/x) больше или равно 5*(1/75)^((7x-x^2-9)/x)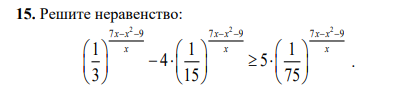

Решите неравенство log 4 (24-12x)≥ log 4 (x^2-7x+10)+ log 4 (x+3)

5) lg(x^(2)-8x+13)>0

4) log_(2)(x+2)+log_(2)(x+3)>log_(2)(1-x)

Решите неравенство log(1/3)(log2(x^2-9)-2) больше или равно -1

Решить неравенство log(1/2)(x-3)+log(1/2)(9-x) больше или равно -3

Решите неравенство
7^(ln(x^2-2x)) ≤ (2-x)^(ln7)

Решите неравенство

5log(16)(x^2+4x-5) ≤ 6+ log(16)(x+5)^5/(x-1)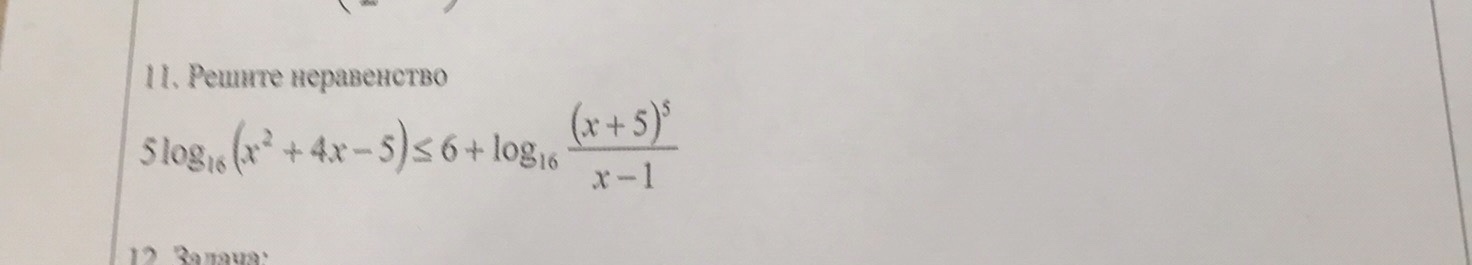

(2^(x+5)-2^-x)/(2^(3-x)-4^-x)≥2^x

Решите неравенство
log(625x) 25 * log^2 (1/5) (25x) ≤2
(log 25 по основанию 625х * log в квадрате 25х по основанию 1/5 ≤2)

Решить неравенство (3*2^(x^2)+2^(-x)) / (4-2^(-x-x^2)) ≤ 2^(1-x)

Решить неравенство

log2(x+1)^2*log(1/3)x^2 - 4log2(x+1) + 4log3(-x) + 4 ≤ 0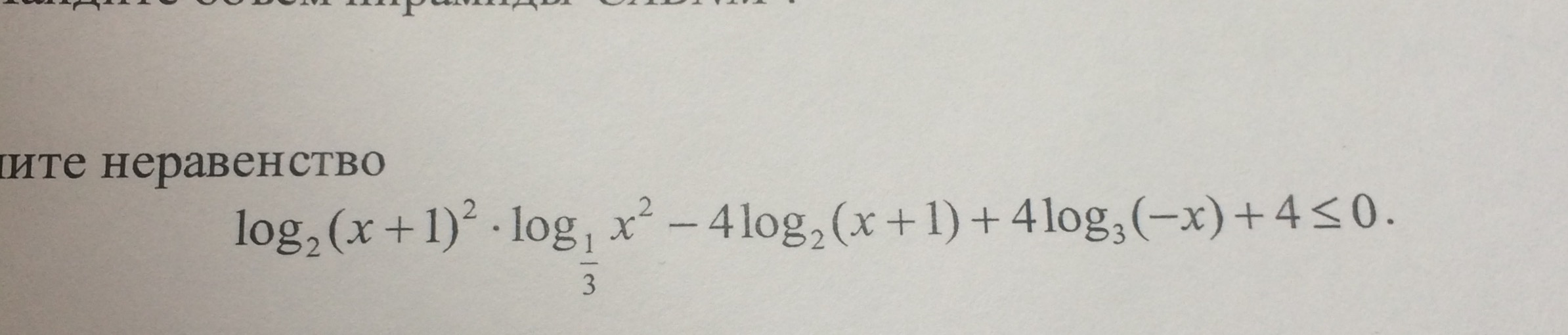

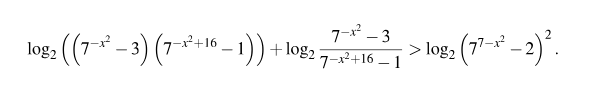
Решить неравенство log7(x^2-16) ≤ 3*log7((x+4)/(x-4))

Решите неравенство 0,5^(-(x-2/2x+4)) × 10^x × x^-2 >= (32^(-(x-2/2x+4)) × 40^x) / 16x^2

log(|x-2|)(3-|x|) ≤ 0

Решить неравенство (log2x-5)/(1-2log2x) ≥ 2log2x

Решить неравенство log2(7^(-x^2)-3)(7^(-x^2+16)-1)) + ...

45/(log^2(2)x - 2log(2)x)^2 - 18/(log^2(2)x - 2log(2)x) +1 < 0

2log2(cos^2x)+7log2(cosx) ≥ 1

(x^2+x)lg(x^2+2x-2)/|x-1| ≥ lg(-x^2 -2x+2)^2/(x-1)

Решите неравенство

log(2x+1) (4x-5) + log(4x-5)(2x+1) ≤ 2

Решите неравенство

Решите неравенство:

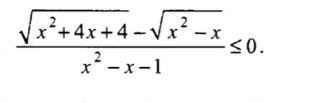
log(4-x) ((x-4)^8) / (x+5) ≥ 8

Решить неравенство log(sqrt(2x^2-7x+6)) (x/3) > 0

помогите, пожалуйста, решить неравенство
log3 (9x) - 13/ log3^2 x + log3 x^4 ≤ 1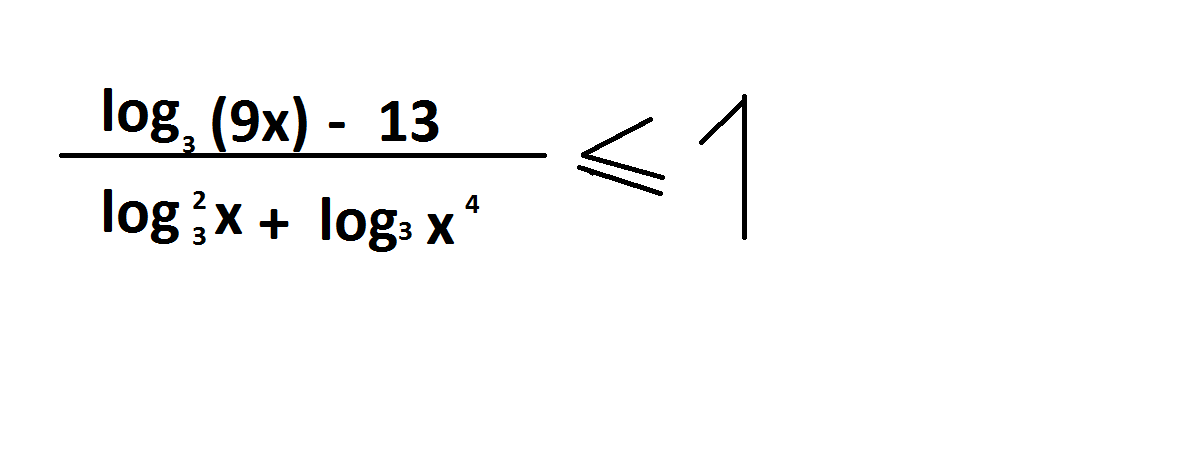

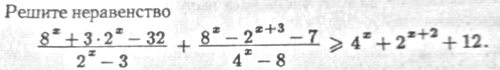
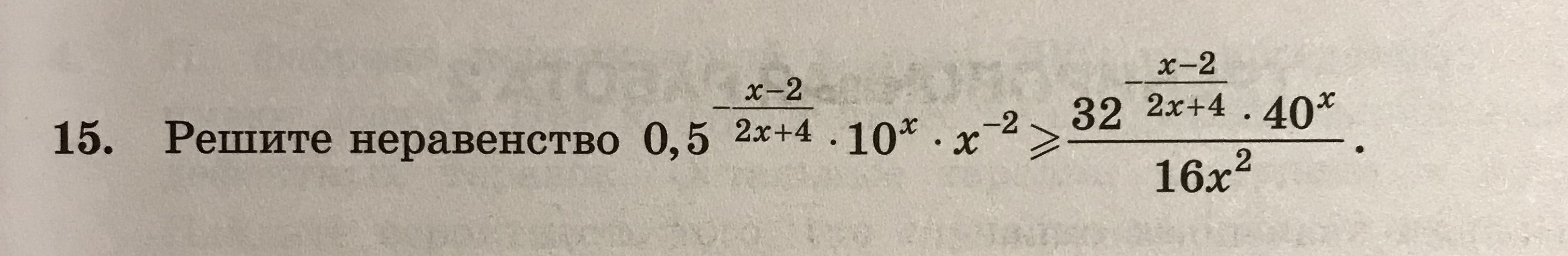
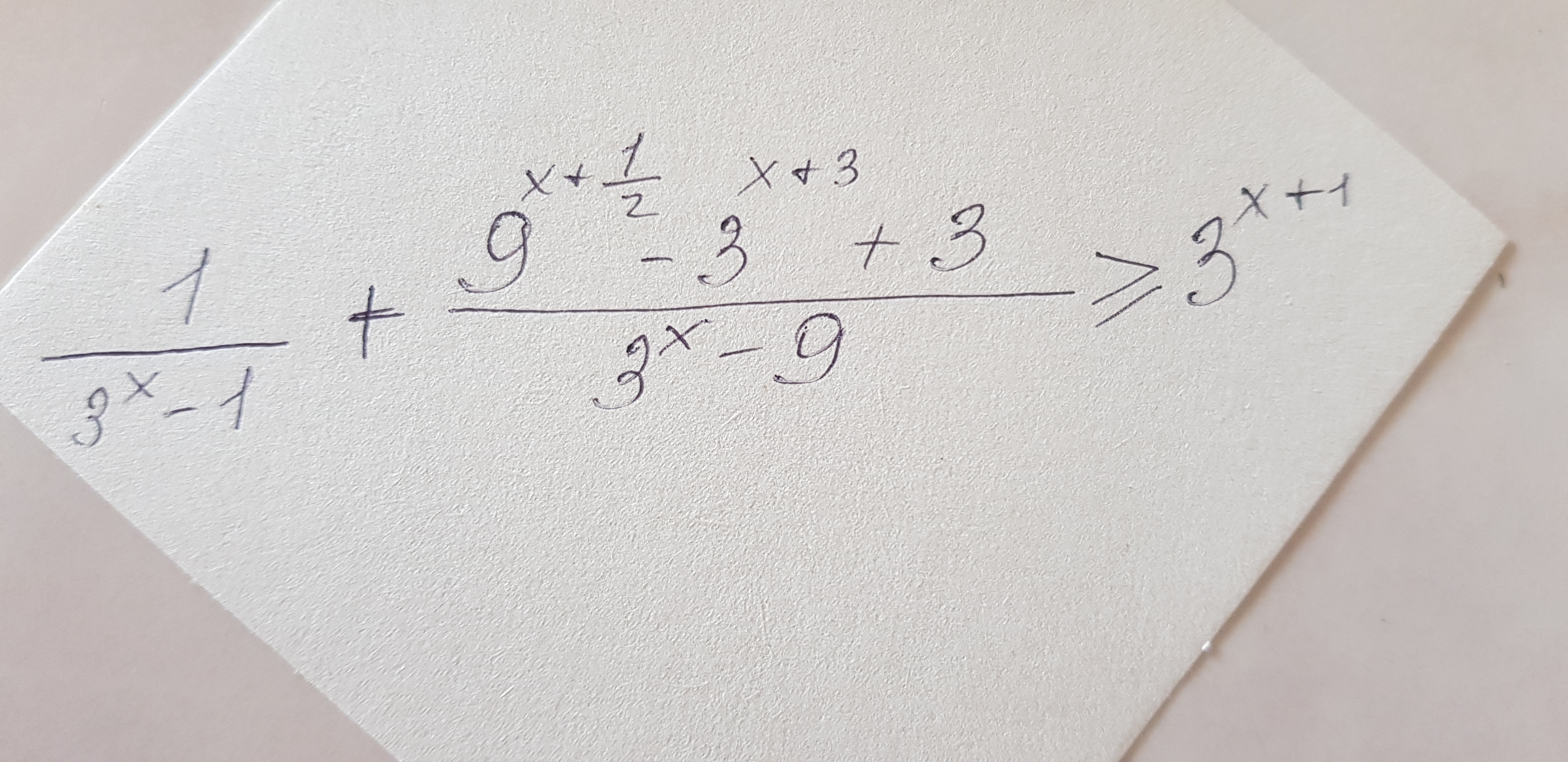
6.49) (lg^2x-3lgx+3)/(lgx-1) меньше или равно 1

6.48) 1/(1+log2x)+1/(1-log2x) > 2

6.47) log3x меньше или равно 2/(log3x-1)

6.44) 2log2x-log2(2x-2) > 1

6.40) 1+log2(2-x) > log2(x^2+3x+2)

6.43) log(1/5)(x^2+6x+18) + 2log5(-x-4) < 0

6.51) log(x)((6-5x)/(4x+5)) > 1

6.52) log((x^(-2)))(x+2) > -1

7.7) 2^x+2^(|x|) больше или равно 2sqrt(2)

7.4) sqrt(x^2-x+4) меньше или равно 2x+|3x+2|

7.5) 5^(75)*(1/5)^x*(1/5)^(sqrt(x)) > 1

7.3) (x^3-8+6x(2-x))/|3-4x| меньше или равно sqrt(4x-3)

log2x-log2(x+2)+log((x+2)/x) 2 > 0 [6.61]

log5sqrt(3x+1)*log(x-1) 5 > 1 [6.59]

((x+0,5)(x+3)) / log2|x+1| < 0 [7.11]

(0,3)^(log5(log(1/5)(x^2-4/5))) < 1 [7.15]

log(1/2)(log8((x^2-1)/(x-2))) < 0 [6.65]

log(1/2)x^2+log3x^2 > 1 [6.66]

0,2^(-2x+3/x-5)*15^(2x)*25x^(-2) ≥ (25^(-2x+3/x-5)*9^x)/5x^2

2log2(xsqrt(2))-log2(x/(1-x)) меньше или равно log2(8x^2+1/x-5)

((x+1)/10)^(lg(x+1)-2) < 100 [7.27]

x^((lg10x)-2) < 100 [7.26]

x^(lg^2x-3lgx+1) > 1000 [7.25]

log(4/3)(sqrt(x+3)-sqrt(x))+log(4/25)(2/5) ≥ 0 [7.33]

sqrt(x^(log2sqrt(x))) ≥ 2 [7.28]

3^((log3x)^2 / 4) ≤ (x^((log3x)/3))/3 [7.29]

5^(log(x)49)-7^(log(x)5)-2 ≥ 0 [7.30]

log2(2^x-1)*log(1/2)(2^(x+1)-2) > -2 [7.50]

log3(log(1/8)((3/2)^(-x)-1/2)) ≤ -1 [7.48]

(4^x-2^(x+3)+7)/(4^x-5*2^x+4) меньше или равно (2^x-9)/(2^x-4)+1/(2^x-6) [7.45]

log(-x)(log9(3^(-x)-9)) < 1 [7.49]

(x+1)/(3-log3(9-3^(-x)) меньше или равно 1 [7.40]

(4^(x^2-x-6)-1)*log(0,25)(4^(x^2+2x+2)-3) меньше или равно 0 [7.43]

log(|x|)(sqrt(9-x^2)+x-1) ≥ 1 [7.52]

log2(1/x-1)+log2(1/x+1) ≤ log2(27x-1)

log(9 корней из 8)(log(1/7)(x+1)) ≥ 3 [v14-15]

log(2x)4x ≤ sqrt(log(2x)(16x^3)) [7.53]

(sqrt(3)-sqrt(2))^((log34)^(4-x^2)) ≤ (sqrt(3)+sqrt(2))^(-(log32)^(2x-1)) [7.60]

Решите неравенство 1+10/(log2x−5)+16/(log^2_(2)x−log2(32x^(10))+30)≥0.

корень 6ой степени из (64^(3x-1)) > sqrt((1/16)^((1-3x)/(x-1))) [v8-15]

Решить неравенство log5((2/x)+2)-log5(x+3) ≤ log5((x+6)/x^2)

Решите неравенство 8^x+3*2^x-32 ...

0,5^(-(x-2)/(2x+4)) * 10^x * x^(-2) ...

1/(3^x-1) + ...

Решить уравнение (2^(4x)-2^(3x+1)+2^(2x+1)-2^(x+1)+1) / ((2^x-2)^2+(2^x-3)^3-1) ≥ 0

Решить неравенство: (x^2+x+1)^(x^2-3x-4) < (x+5)^(x^2-3x-4)

Решить неравенство ((x^2+x)lg(x^2+2x-2))/|x-1| ≥ (lg(-x^2-2x+2)^2)/(x-1)

решите неравенство

(64^x-7*16^x) /(4^x +1) +(6*16^x - 3*4^(x+2) ) /(4^x- 6) +42>=0

[block] (log4(x^4-4x^3+4x^2)-log4(6x^2-12x-9))/(x^2-2x-8) ≥ 0 [/block]

Решите неравенство

log(x) (x+1)/(12x) > 2log((x+1)/12) x [L15]

[block](x-3)(log6(x^2+3x-4) + log(0,2)(20-5x)+ (1)/(log(4-x) 5)+x+1) ≥ x^2-x-6[/block]

[block]Решить неравенство: log_(x+3)(x^2+4x+5)/(|3x+5|) ≥ 0[/block]

[block](log(x+1)x)/(log(x+1)(3x+2)) < 1[/block]

Решите логарифмическое неравенство

log((2x+2)/(5x-1)) (10x^2+x-2) ≤ 0

log5(25x) / log5x-2 ...

log2(5-x)*log(x+1) 1/8 ≥ -6

[block](1)/(log(x-3) x/10) ≥ -1[/block]

[block](2log9(x^2+4x))/(log9x^2) ≤ 1[/block]

решить неравенство

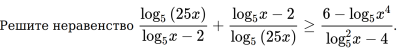
log(1+1/(x+1)^2) (x^2+3x+2 / x^2-3x+4) ...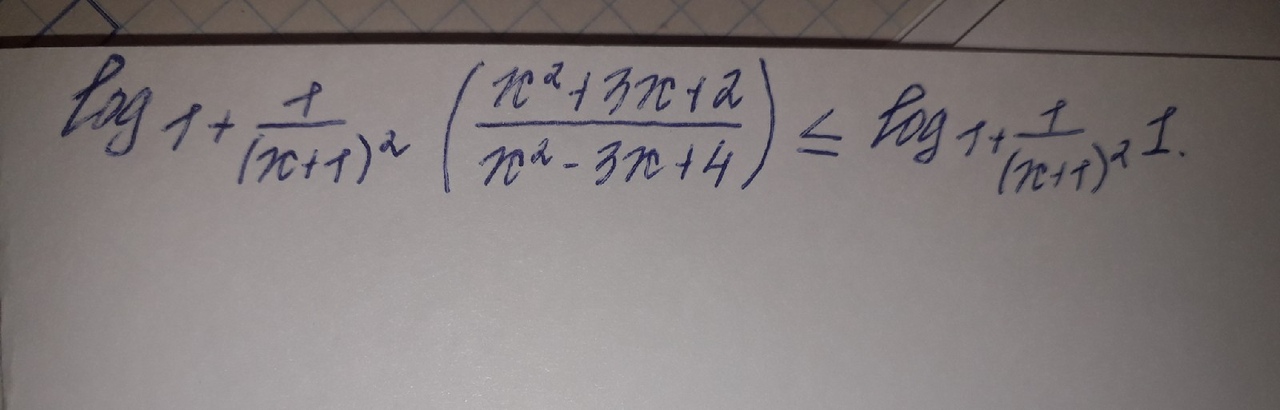

log^2_(2) (-log3x) + log2log^2_(3) x ≤ 8

Решите неравенство

log(1/3)(x^2-3x-1) + log(1/3)(2x^2-3x-2) ≤ log(1/3)(x^2-2x-1)^2 + log34 - 2

Решите неравенство

5^(x+2) + 5^(x+1) - 5^x < 3^((x/2) + 1) - 3^(x/2) - 3^((x/2) - 1)

(x^2+3x+2) * log(x+3)(x+2) * log3(x-1)^2 ≤ 0

Решите пожалуйста неравенство 5^(х+2)+5^(х+1)-5^х<3^(x/2+1)-3^(х/2)+3^(х/2-1)

log(4-x) (x+3)*log(x+5) (3-x)≥0

[block]Решите неравенство (2)/(5^x-1) + (5^x-2)/(5^x-3) больше или равно 2[/block]

Решите неравенство log4(x^2-4)^2+log2(x-1)/(x^2-4) > 0

Решите неравенство

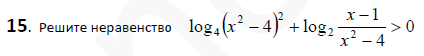
log2(8x^2) + 2log2x + 12 ...

2^(lg(cos(-6π))) ≥ log(x^2) (2x^2-6x+9)

Решить неравенство log3(81^x+16^x-18*4^x+32) ≥ 4x

Решить неравенство log(x)(x-1)*log(x+1)(x-1) < 0

Решить неравенство (x^2-1)^(2+x) > (x^2-1)^(5x-3)

Решить неравенство log2(x+1)^2*log(1/3)x^2 - 4log2(x+1) + 4log3(-x) + 4 меньше или равно 0

[block](2log(2^(x-1)) x)/(log(2^(x-1))(x+7)) меньше или равно (log3(x+12))/(log3(x+7))[/block]

Решить неравенство log2(2^x-1)*log(1/2)(2^(x+1)-2) > -2

Решить неравенство

log(1,5x+1)(3x+7)*log(1+(3x/2))((24x+56)/(3x+2)^3) меньше или равно -2

Решите неравенство

log^2_(0,5) (4x) * log(0,25) (0,25x)^2 ≤ log(0,5)5*log5(x/4)

log2(1-(1/x))+log2(10-x) ≤ 2

Решить неравенство

(log(2^(x+4)) 4) / (log(2^(x+4)) (-8x)) меньше или равно 1/(log2log(1/2) 2^x)

1) lg(x^2+2x+2) < 1

3) log(1/3)(x^2+3x-1) < -1

Решить неравенство 1/(1+2^x) - 2/(4^x-2^x+1) < (1-2^(x+1))/(8^x+1)

log(x^2–3) (x^2+6) ≥ log(x^2–3) (7) + log(x^2–3) (x)

log(x^2) (3-x) ≤ log(x+2) (3-x)

(log(x) 2- 1) * log2 (2x) ≤ 3/2

log(x^2-3) (x^2+6) ≥ log(x^2-3) (7)+ log(x^2-3) (x)

Решить неравенство log(16/(25-x^2))(14/(24-2x-x^2)) > 1

(log4(16x^4)+11)/(log^2_(4)x-9) больше или равно -1

log3(81^x+16^x-18*4^x+32) больше или равно 4x

Решите неравенство: 9/(3+ log3x *log3 9/x) ≤ logx^2 3 - log3 x^2/27

Решите неравенство: log_((x+4)^2) (3x^2-x-1) ≤ 0

Решите неравенство: (2^x - 2)^3 / (2^(x+2) - 12) ≥ (8^x - 4^(x+1) + 2^(x+2))/(9-4^x)

Решить неравенство log5(3x+1)+log5((1/72x^2)+1) ≥ log5((1/24x)+1)

Решить неравенство log^2_(3)(-log3x)+log3log^2_(3)x ≤ 3

Решите неравенство

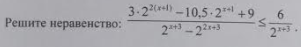
log2(x+2)-log2(x-1) < 1-log2(5-x)

Решите неравенство

log2(3-2x) + 2log2(1/x) ≤ log2((1/x^2) - 2x + 2)

Решить неравенство

log^2_(2)(3x-1) + log^2_(3x-1)2 - log2(3x-1)^2 - log_(3x-1)4 + 2 меньше или равно 0

Решить неравенство (x-3)sqrt(x^2-6x+8) меньше или равно 0

Решить неравенство

log(sinx+cosx+4) (x^2+1) ≥ log(2sinx*cosx+4,5) (x^2+1)

Решить неравенство

5lg(x^2+3x+2) меньше или равно 6+lg((x+2)^5/(x+1))

logx(4-x)*logx(x+1) ≥ 0

Решите неравенство (log2(3*2^(x-1)-1)) / x больше или равно 0

Решите неравенство (3log9x+1)/(2log9x+3) меньше или равно 3-log9x

Решите неравенство (log2(2x^2-17x+35)-1) / log7(x+6) меньше или равно 0

Решите уравнение 2(x-3)^2+(x-3)sqrt(x) > x

Решите неравенство log(x-2)(x^2-6x+8) > log(x-3)(x^2-6x+8)

Решите неравенство log3(2-3^(-x)) < x+1-log34

Решите неравенство log3(4-3^x) < -x-2+log311