Задача 62506 Решите...

61d30159f9ee7a38ce6b111f

03.01.2022 17:01:15

Решите неравенство

[block]log2((7^(-x^2)-6)(7^(-x^2+9)-1)) + log2 (7^(-x^2)-6)/(7^(-x^2+9)-1) > log2(7^(3-x^2)-5)^2[/block]

5f3ea7e3faf909182968ddd9

04.01.2022 13:07:01

Запишем ОДЗ:

[m]\left\{\begin {matrix}(7^{-x^2}-6)(7^{-x^2+9}-1)>0\\\frac{7^{-x^2}-6}{7^{-x^2+9}-1}>0\\(7^{3-x^2}-5)^2>0 ⇒ 7^{3-x^2}-5 ≠ 0\end {matrix}\right.[/m]

Так как [m] -x^2 ≤ 0[/m] ⇒[m] 7^{-x^2} ≤ 1[/m]

и потому
[m] 7^{-x^2}-6<0[/m], значит вместо первого и второго неравенств системы получаем только одно неравенство:

[m]7^{-x^2+9}-1<0[/m] ⇒ [m]7^{-x^2+9}<1[/m] ⇒ [m]7^{-x^2+9}<7^{0}[/m]

Показательная функция с основанием [m]7>1 [/m] [i]возрастающая [/i] ⇒

[blue][m]-x^2+9 <0[/m][/blue] ⇒

[m]x^2-9>0[/m]

[m](x-3)(x+3) >0[/m]

[red][m]x ∈ (- ∞ ;-3) \cup (3;+ ∞ )[/m][/red]


Третье неравенство системы, определяющей ОДЗ:

[m]7^{3-x^2}-5 ≠ 0[/m] ⇒

[m]7^{3-x^2} ≠ 5[/m] ⇒

[m]7^{3-x^2} ≠7^{log_{7}5}[/m] ⇒

[m]3-x^2 ≠log_{7}5[/m]

[m]x^2 ≠ 3-log_{7}5[/m]

[m]x ≠ ± \sqrt{ 3-log_{7}5}[/m]


так как
[m]3-log_{7}5= log_{7}7^3-log_{7}5= log_{7}\frac{7^3}{5}[/m]

Так как [m]2=log_{7}7^2<log_{7}\frac{7^3}{5}<log_{7}7^{3}=3[/m] ⇒[m] \sqrt{2} <|\sqrt{ 3-log_{7}5}|<\sqrt{3}[/m] ⇒

[m]± \sqrt{ 3-log_{7}5} ∉ [/m][red][m] (- ∞ ;-3) \cup (3;+ ∞ )[/m][/red]

Таким образом

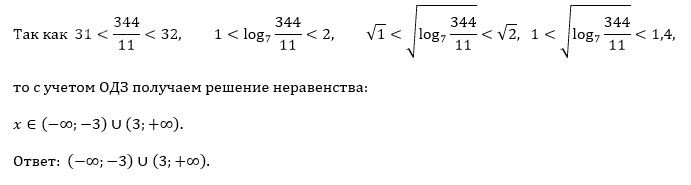
ОДЗ:[red][m]x ∈ (- ∞ ;-3) \cup (3;+ ∞ )[/m][/red]


[b]Решение неравенства:[/b]

[m]log_{2}(7^{-x^2}-6)(7^{-x^2+9}-1)+log_{2}\frac{7^{-x^2}-6}{7^{-x^2+9}-1}>log_{2}(7^{3-x^2}-5)^2[/m]

В условиях ОДЗ заменим сумму логарифмов логарифмом произведения

[m]log_{2}(7^{-x^2}-6)(7^{-x^2+9}-1)\cdot (\frac{7^{-x^2}-6}{7^{-x^2+9}-1})>log_{2}(7^{3-x^2}-5)^2[/m]

[m]log_{2}(7^{-x^2}-6)^2>log_{2}(7^{3-x^2}-5)^2[/m]


Логарифмическая функция с основанием 2>1 возрастающая, получаем:

[m](7^{-x^2}-6)^2>(7^{3-x^2}-5)^2[/m]

Покажем, что неравенство верно при всех х, принадлежащих ОДЗ: [red][m]x ∈ (- ∞ ;-3) \cup (3;+ ∞ )[/m][/red]



При нахождении ОДЗ было получено неравенство:

[blue][m]-x^2+9 <0[/m][/blue] ⇒ [m]-x^2 <-9[/m] ⇒

[b][m]0 < 7^{-x^2} < 1[/m][/b]

[m]-6 < 7^{-x^2}-6 < -5[/m]

[b][m]25 < (7^{-x^2}-6)^2 < 36[/m][/b]


[m]0 < 7^{3-x^2} <1 [/m]

[m]-5 < 7^{3-x^2}-5 <-4 [/m]

[b][m]16 < (7^{3-x^2}-5)^2 <25[/m][/b]



Очевидно, что из полученных оценок: [m] (7^{-x^2}-6)^2 ∈ (25;36)[/m] и [m] (7^{3-x^2}-5)^2 ∈ (16;25)[/m]


при любых [red][m]x ∈ (- ∞ ;-3) \cup (3;+ ∞ )[/m][/red]

[m](7^{-x^2}-6)^2>(7^{3-x^2}-5)^2[/m]