Задача 29950 корень 6ой степени из (64^(3x-1)) >...
Условие
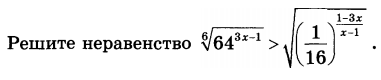
математика 10-11 класс
10732
Решение
★
корень 6-ой степени из 64^(3x–1)=(2^6)^(3x-1)/6=2^(3x-1)
sqrt((1/16)^(1-3x)/(x-1))=sqrt((2^(-4))^((1-3x)/(x-1))=
=(2)^(-2*(1-3x)/(x-1))
Неравенство принимает вид:
2^(3x-1) > (2)^(-2(1-3x)/(x-1))
Показательная функция с основанием 2>1 возрастает, поэтому
3х - 1 > -2*(1-3x)/(x-1);
(3x-1)*(1-(2/(x-1))) >0
(3х - 1)*(х - 3)/( х - 1) > 0
Применяем метод интервалов:
_-__ (1/3) ___+____ (1) __-_ (3) ___+___
О т в е т. (1/3;1) U(3;+ ∞ )
Все решения

