Задача 57646 Помогите......
Условие
Решение
[m]cos(\frac{5π}{2}+x)=-sinx[/m]
Уравнение:
[m]2(-sinx)^2+\sqrt{2}\cdot sinx=0[/m]
[m]2sin^2x+\sqrt{2}\cdot sinx=0[/m]
[m]sinx\cdot (2sinx+\sqrt{2})=0[/m]
[m]sinx=0[/m] или [m]2sinx+\sqrt{2}=0[/m]
[m]sinx=0[/m] ⇒[m] x=πk, k ∈ [/m][b]Z[/b]
ИЛИ
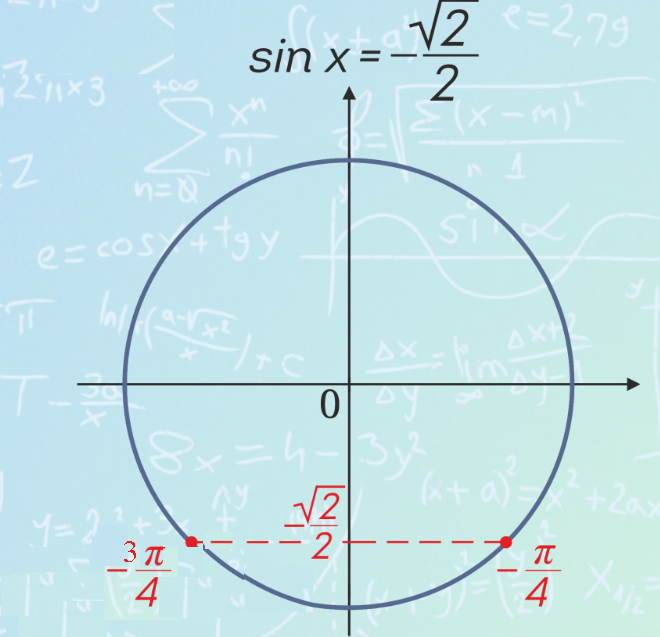
[m]2sinx+\sqrt{2}=0[/m] ⇒ [m]sinx=-\frac{\sqrt{2}}{2}[/m] ⇒[m]x=(-1)^{k}(-\frac{π}{4})+πk, k ∈ [/m][b]Z[/b]
Запишем как две серии:
[m]x=-\frac{π}{4}+2πn, n ∈ [/m][b]Z[/b] или [m]x=-\frac{3π}{4}+2πm, m ∈ [/m][b]Z[/b]
(Очень полезно, [b]особенно при отборе корней[/b], записывать решение уравнения sinx=a в виде двух серий с периодом 2π)
Итак, получили три серии корней. Это и есть О Т В Е Т
[m] x=πk, k ∈ [/m][b]Z[/b]
ИЛИ
[m]x=-\frac{π}{4}+2πn, n ∈ [/m][b]Z[/b] или [m]x=-\frac{3π}{4}+2πm, m ∈ [/m][b]Z[/b]
2)
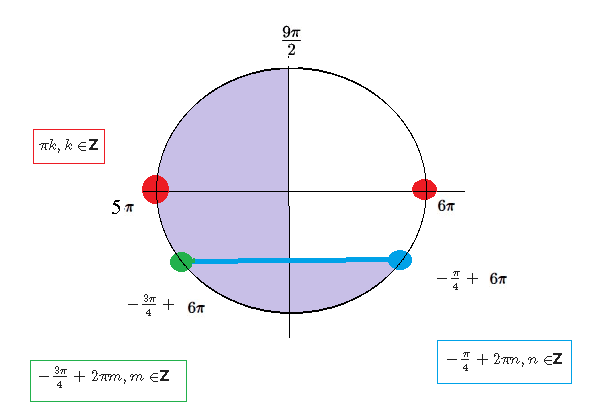
Отбор корней проведем на единичной окружности.
См. рис. 2
Из серии [m] x=πk, k ∈ [/m][b]Z[/b]
[m]x=5π ∈ [\frac{9π}{2};6π][/m]
Из серии [m]x=-\frac{3π}{4}+2πm, m ∈ [/m][b]Z[/b]
[m]x=-\frac{3π}{4}+6π =\frac{21π}{4} ∈ [\frac{9π}{2};6π][/m]
Из серии [m]x=-\frac{π}{4}+2πn, n ∈ [/m][b]Z[/b]
[m]x=-\frac{π}{4}+6π =\frac{23π}{4} ∈ [\frac{9π}{2};6π][/m]
