Задача 33379 ...
Условие
log(1/3)(x^2-3x-1) + log(1/3)(2x^2-3x-2) ≤ log(1/3)(x^2-2x-1)^2 + log34 - 2
Решение

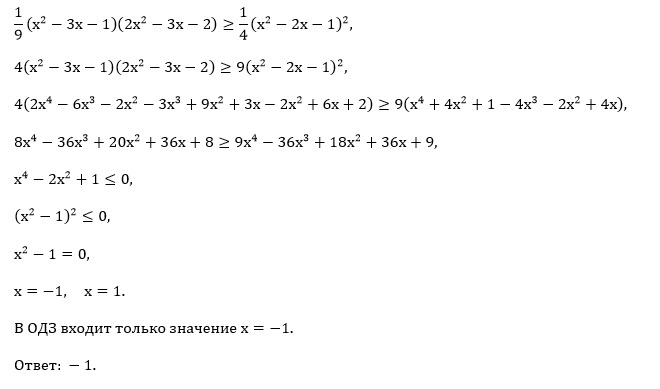
Все решения
{x^2-3x-1>0 ⇒ D=13; x_(1)=(3-sqrt(13))/2 ; х_(2)=(3 sqrt(13))/2⇒x< x_(1) или x > x_(2)
{2x^2-3x-2>0 ⇒ D=25; x_(3)=-1/2; x_(4) =2⇒ x < x_(3) или х > x_(4)
{(x^2-2x-1)^2 >0 ⇒ x^2-2x-1 ≠ 0 ⇒ D=8 ⇒ x ≠ 1-sqrt(2); x ≠ 1 sqrt(2)
[b]Сравниваем[/b] ( между числами можно поставить любой знак: звездочка; больше; меньше и применять все правила действий с неравенствами)
(3+ sqrt(13))/2 [b]и[/b] 1+sqrt(2)
Умножаем на2
3+ sqrt(13) [b]и[/b] 2+ 2sqrt(2)
Уменьшаем обе части на2
1+ sqrt(13) [b]и[/b] 2*sqrt(2)
Возводим в квадрат
1 +2sqrt(13) +13) [b] и[/b] 8
ясно, что число слева больше
[b]1+ sqrt(2) < (3+ sqrt(13))/2[/b]
2 < 1+ sqrt(2), так как
2-1< 1-1+ sqrt(2)
1 < sqrt(2)
возводим в квадрат
1 < 2
Значит
2< 1 + sqrt(2) < (3 + sqrt(13))/2
Аналогично
(-1/2) < 1- sqrt(2)
sqrt(2) < (3/2)
2 < 9/4 - верно
1-sqrt(2) < (3-sqrt(13))/2;
2-2sqrt(2) <3-sqrt(13);
sqrt(13)< 3-2 +2sqrt(2)
13 < 1+ 4sqrt(2) +8
13-1-8 < 4 sqrt(2)
4< 4 sqrt(2) - верно.
ОДЗ: х ∈ (- ∞ ; -1/2) U ((3 sqrt(13))/2; ∞ )
Применяем формулу перехода в другому основанию:
переходим к основанию 3
-log_(3)(x^2-3x-1) - log_(3)(2x^2-3x-2) ≤ - log_(3)(x^2-2x-1)^2 log_(3)4 -log_(3)9
log_(3)(x^2-2x-1)^2 log_(3)9 ≤ log_(3)(x^2-3x-1) log_(3)(2x^2-3x-2) log_(3)4
log_(3)(x^2-2x-1)^2*9 ≤ log_(3)(x^2-3x-1)*(2x^2-3x-2)*4
3>1 Логарифмическая функция возрастает
9*(x^2-2x-1)^2 ≤ 4*(x^2-3x-1)*(2x^2-3x-2);
9*(x^4+ 4x^2+ 1-4x^3-2x^2+ 4x) ≤ 4(2x^4-6x^3-2x^2-3x^3+ 9x^2 +3x-2x^2+ 6x+ 2)
x^4 -2x^2+ 1 ≤ 0
(x^2-1)^2 ≤ 0
неравенство верно лишь при x^2-1=0
x= ± 1
x=1 ∉ ОДЗ
О т в е т. -1

