Задача 33263 ...
Условие
Решение
{x^2+4x>0 ⇒ x*(x+4) > 0 ⇒ x < -4 или х > 0
{x^2>0 ⇒ x ≠ 0
{log_(9)x^2 ≠ 0 ⇒ x^2 ≠ 1 ⇒ x ≠ ± 1
ОДЗ: (- ∞ ;-4) U(0;1) U(1;+ ∞ )
Разделим обе части неравенства на 2:
log_(9)(x^2+4x)/log_(9)x^2 ≤ 1/2
Применяем формулу перехода к другому основанию ( справа налево, cм приложение 1)
log_(x^2)*(x^2+4x) ≤ 1/2;
log_(x^2)(x^2+4x) ≤ (1/2) * log_(x^2)(x^2);
log_(x^2)*(x^2+4x) ≤ log_(x^2) sqrt(x^2)
Применяем метод рационализации логарифмических неравенств ( см таблицу)
(x^2-1) *(x^2+4x-|x|) ≤ 0
При x > 0
(x-1)(x+1)(x^2+3x) ≤0
x(x-1)(x+1)(x+3) ≤ 0
(0) _-_ [1] __+__
c учетом ОДЗ
x ∈ (0;1)
При x <0
(x-1)(x+1)(x^2+4x+x) ≤ 0
(x-1) (x+1) (x+5)*x ≤ 0
_+__ [-5] ___-__ [-1] __+__ (0)
[-5; -1]
c учетом ОДЗ:
[-5;-4)
О т в е т. [-5;-4) U(0;1)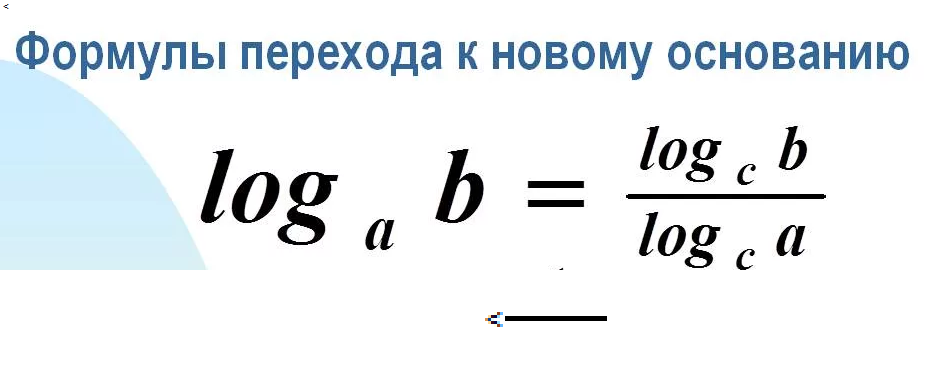

Все решения

