Задача 63824 ...

624318ad899c0b5ef5d7f224

29.03.2022 17:43:37

Решить неравенство

|x^3 - 2x^2 + 2| ≥ 2 - 3x

5f3ea7e3faf909182968ddd9

29.03.2022 20:28:52

★

По определению модуля.

2 случая.

1)
x^3-2x^2+2 ≥ 0 ⇒ |x^3-2x^2+2 |=x^3-2x^2+2
x^3-2x^2+2 ≥ 2-3x

2)x^3-2x^2+2 < 0 ⇒ |x^3-2x^2+2 |=-(x^3-2x^2+2 )
-(x^3-2x^2+2) ≥ 2-3x

Получаем две системы неравенств:

[m]\left\{\begin {matrix}x^3-2x^2+2 ≥ 0\\x^3-2x^2+2 ≥ 2-3x\end {matrix}\right.[/m] ИЛИ [m]\left\{\begin {matrix}x^3-2x^2+2 < 0\\-(x^3-2x^2+2) ≥ 2-3x\end {matrix}\right.[/m]

[m]\left\{\begin {matrix}x^3-2x^2+2 ≥ 0\\x^3-2x^2+3x ≥0\end {matrix}\right.[/m] ИЛИ [m]\left\{\begin {matrix}x^3-2x^2+2 < 0\\x^3-2x^2-3x+4 ≤ 0\end {matrix}\right.[/m]

[m]\left\{\begin {matrix}x^3-2x^2+2 ≥ 0\\x\cdot (x^2-2x+3) ≥0; D=4-12 <0\end {matrix}\right.[/m] ИЛИ [m]\left\{\begin {matrix}x^3-2x^2+2 < 0\\x^3-2x^2-3x+4 ≤ 0\end {matrix}\right.[/m]

[m]\left\{\begin {matrix}x^3-2x^2+2 ≥ 0\\x≥0\end {matrix}\right.[/m] ИЛИ [m]\left\{\begin {matrix}x^3-2x^2+2 < 0\\x^3-2x^2-3x+4 ≤ 0\end {matrix}\right.[/m]

Решаем первую систему

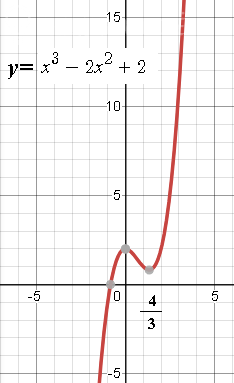
Строим график
y=x^3-2x^2+2

y`=3x^2-4x

x=0; x=4/3

y(0)=2

y(4/3)=(4/3)^2-2*(4/3)^2+2=

см. рис.



y=x^3-2x^2+2 пересекает ось Ох в точке x_(o)

-1 <x_(o)< 0

y(0)=2

y(-1)=(-1)^3-2*(-1)^2+2=-1-2+2

На концах [-1;0] функция принимает значения разных знаков, значит, x_(o)- внутри [-1;0]

Первому неравенству удовлетворяет та часть, которая выше оси ОХ

т. е при x > x_(o)


Второе неравенство [m] x ≥ 0[/m]

Решение первой системы : [m] x ≥ 0[/m]


Решаем вторую систему

График уже построен.

Первому неравенству удовлетворяет та часть, которая ниже оси ОХ

Решаем второе неравенство

[m]x^3-2x^2-3x+4 ≤ 0[/m]

x=1 является корнем уравнения [m]x^3-2x^2-3x+4 =0[/m]

Значит левая часть раскладывается на множители

[m](x-1)(x^2-x-4)≤ 0[/m]

D=1+16=17

[m]x_{1}=\frac{1-\sqrt{17}}{2}[/m] или[m]x_{2}=\frac{1-\sqrt{17}}{2}[/m]

и третий корень [m]x_{3}=1[/m]

_____-____ [m][\frac{1-\sqrt{17}}{2}][/m] __+____ [1] ___-___[m] [ \frac{1+\sqrt{17}}{2}][/m] ___+___

Решение второго неравенства второй системы
[m] (- ∞ ;\frac{1-\sqrt{17}}{2}] \cup [1; \frac{1+\sqrt{17}}{2}][/m]

С учетом того, что первому неравенству удовлетворяет та часть графика , которая ниже оси ОХ

т. е при x < x_(o)

[m] (- ∞ ;\frac{1-\sqrt{17}}{2}] < -1 < x_{o}[/m]

Ответ второй системы: [m] (- ∞ ;\frac{1-\sqrt{17}}{2}] [/m]


О т в е т. [red][m] (- ∞ ;\frac{1-\sqrt{17}}{2}] \cup [0; + ∞) [/m][/red]