Задача 32075 ...
Условие
log3 (9x) - 13/ log3^2 x + log3 x^4 ≤ 1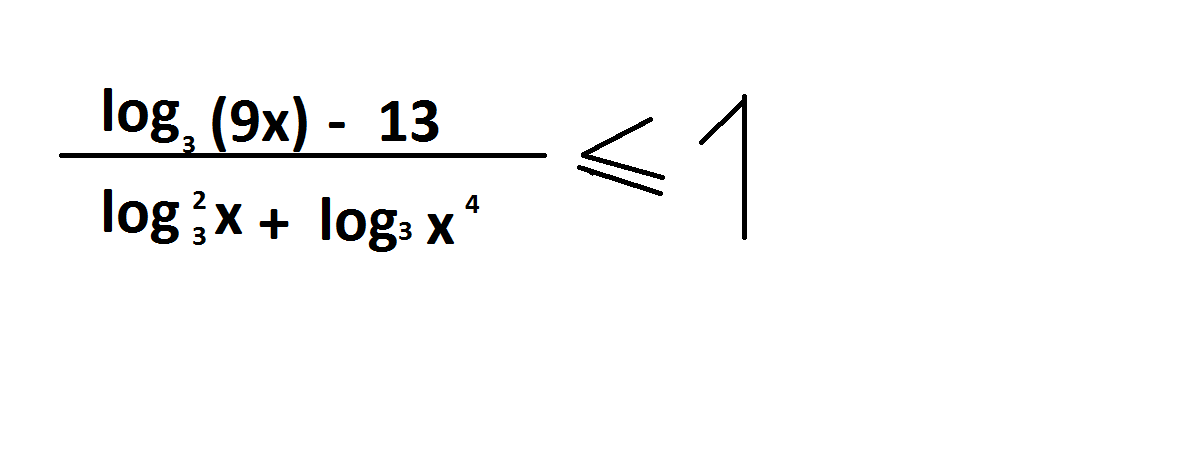
математика 10-11 класс
17889
Решение
★
x>0
В условиях ОДЗ
log_(3)x^4=4log_(3)|x| =4log_(3)x
log_(3)(9x)=log_(3)9+log_(3)x=2+log_(3)x
Замена переменной:
log_(3)x=t
(2+t-13)/(t^2+4t) ≤ 1
(t-11-t^2-4t)/(t^2+4t) ≤ 0
-(t^2+3t+11)/(t^2+4t) ≤ 0
t^2+3t+11 > 0 при любом t, D=9-44 <0
⇒
t^2+4t > 0
_+__ (-4) ___ (0) _+__
log_(3)x <-4 или log_(3)x >0
0<x <1/81 или х > 1
О т в е т. (0;1/81)U(1;+ ∞)
