Задача 38514 Решите...
Условие
[m]\frac{(x^2-x-14)^2}{2x+\sqrt{21}} \leq \frac{(2x^2+x-13)^2}{2x+\sqrt{21}} [/m]
Решение

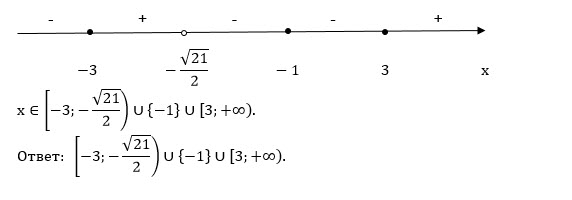
Все решения
Приводим к общему знаменателю:
((x^2-x-14)^2-(2x^2+x-13)^2)/(2x+sqrt(21)) ≤ 0
В числителе применяем формулу разности квадратов:
a^2-b^2=(a-b)(a+b)
(x^2-x-14-2x^2-x+13)(x^2-x-14+2x^2+x-13)/(2x+sqrt(21)) ≤ 0
(-x^2-2x-1)(3x^2-27)/(2x+sqrt(21)) ≤ 0
(x+1)^2(x-3)(x+3)/(2x+sqrt(21)) ≥ 0
Решаем методом интервалов.
Находим нули числителя:
(x+1)^2=0 или х-3=0 или х+3=0
х=-1 или x=3 или х=-3
Отмечаем на числовой прямой закрашенным кружком ( на рисунке квадратные скобки)
Находим нули знаменателя:
2х+sqrt(21)=0
x=-sqrt(21)/2
Отмечаем на числовой прямой пустым кружком ( на рисунке - круглые скобки)
Сравниваем:
-3 < -sqrt(21)/2
так как
3 > sqrt(21)/2 или 6 > sqrt(21) или 36> 21
Рассставлям знаки справа от точки 3 +
Далее знаки чередуем справа налево.
При переходе через точку
x = - 1 нет чередования, так как множитель (x+1) в четной степени:
___-__[-3] _+__ (-sqrt(21)/2) _-_ [-1] _-__ [3] __+__
О т в е т. [-3; -sqrt(21)/2) U{-1} U [3;+ ∞ )
