О категории
Приложение производной. Действия с функциями.
Практика (21)
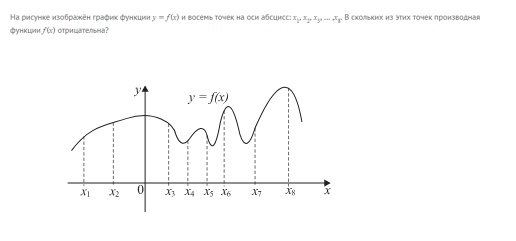
На рисунке изображен график функции y = f(x) и восемь точек на оси абсцисс x: x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈. В скольких из этих точек производная функции f'(x) отрицательна?
На рисунке изображён график у = f’(x) – производной функции f(x), определённой на интервале (-6, 9). Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.

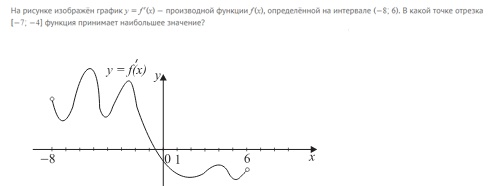
На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (−8; 6). В какой точке отрезка [−7;−4] функция принимает наибольшее значение?
Прямая y = -x - 3 является касательной к графику функции y = x^3 - 3,5x^2 + x - 1. Найдите абсциссу точки касания.
На рисунке изображён график функции y = f(x), определённой на интервале (-2; 7). Определите количество целых точек, в которых производная функции отрицательна.

На рисунке изображён график функции y = f(x) и касательная к этому графику в точке с абсциссой, равной -3. Найдите значение производной этой функции в точке х₀ = -3.

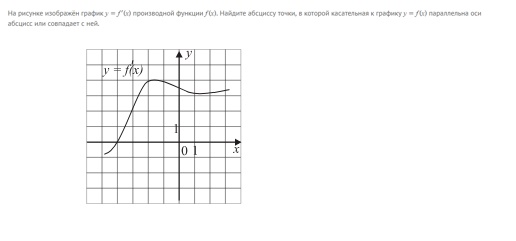
На рисунке изображён график y = f'(x) произведной функции f(x). Найдите абсциссу точек, в которой касательная к графику y = f(x) параллельна оси абсцисс или совпадает с ней.
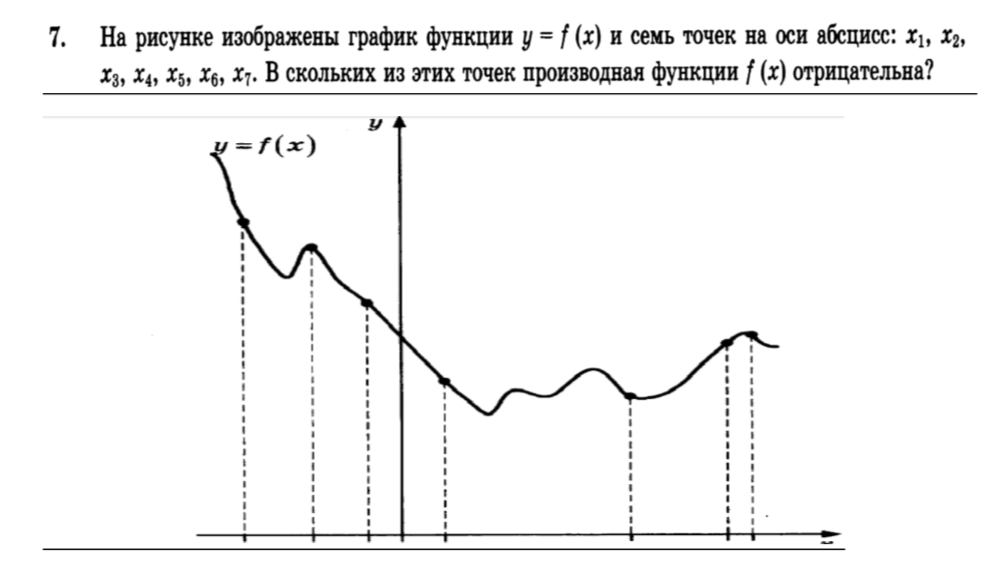
На рисунке изображены график функции [m] y = f(x) [/m] и семь точек на оси абсцисс: [m] x_1, x_2, x_3, x_4, x_5, x_6, x_7 [/m]. В скольких из этих точек производная функции [m] f(x) [/m] отрицательна?
Найдите угловой коэффициент касательной, проведенной к функции:
f(x) = 2/x + 3 в точке с абсциссой, равной x₀ = 2
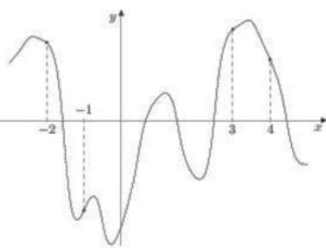
На рисунке изображен график функции у = f(x) и отмечены точки -2, -1, 3,4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
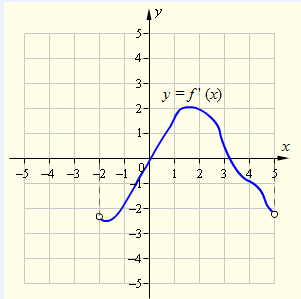
Функция y=f(x) определена на промежутке (-2;5). На рисунке изображен график ее производной. Укажите точку минимума функции y=f(x) на этом промежутке.
На рисунке изображён график y=f'(x) — производной функции f(x), определенной на интервале (-8;4). В какой точке отрезка [-7;-3] функция f(x) принимает наименьшее значение?

Функция у = f(x) определена на всей числовой прямой и является периодической с периодом 5. На промежутке (-1;4] она задается формулой f(x) = 3-|1-x|. Найдите значение выражения 5f(20)-3f(-12). (Л7)
Пусть f '(x) = (6x^2-51x+99)/(x-1) . Чему тогда равно число промежутков убывания функции f(x)?
Найдите наименьшее значение функции y=x+36/x на отрезке [1;9]
Найдите угловой коэффициент касательной к графику функции f(x)=x^2-6x+5, x_(0)=2
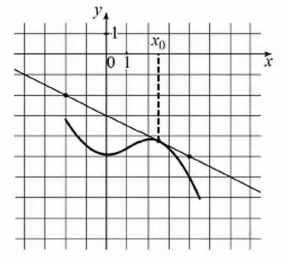
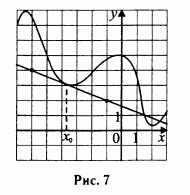
На рисунке 7 изображён график функции у = f(х) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке х0.
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0 .

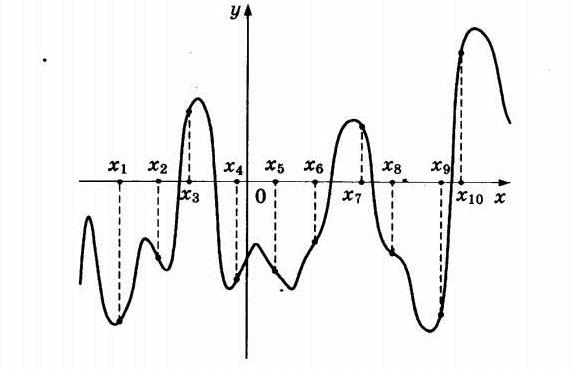
На рисунке изображён график функции y=f(x) и десять точек на оси абсцисс: х1, х2, х3, ..., х10. В скольких из этих точек производная f'(x) функции f(x) положительна?
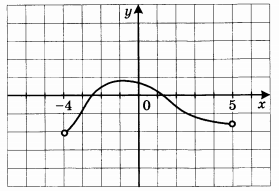
На рисунке изображен график производной функции у = f(x), определенной на промежутке (-4; 5). Найдите количество точек экстремума функции у = f(x).
На рисунке изображены график функции у = f(x) и касательная к нему в точке с абсциссой x_(0). Найдите значение производной функции f(x) в точке