задание 8 (стереометрия)

Простая стереометрия. Работа с объемными фигурами.

В сосуде, имеющем форму конуса, уровень жидкости достигает 0,25 его высоты. Объём жидкости равен 5 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?

Конус и шар имеют равные объемы. Найдите радиус конуса, если его высота 20 см, а радиус шара 5 см.

Найдите объем многогранника, вершинами которого являются точки параллелепипеда ABCDA1B1C1D1, у которого АВ=6. ВС=7, BB1 =9

Образующая конуса наклонена к плоскости основания под углом 30° . Найдите
объем конуса, если площадь сечения, которое проходит через две образующие,
угол между которыми 120 ° , равна 4 корня из 3 см².

Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые). Числа на рисунке обозначают длины рёбер в сантиметрах. Найди объём этой детали. Ответ дай в кубических сантиметрах.

Два ребра прямоугольного параллелепипеда равны 7 и 4, а объём параллелепипеда равен 140. Найди площадь поверхности этого параллелепипеда.

Ответ:

Вычислите объем правильной усеченной треугольной пирамиды, если стороны ее оснований равны 6 см и 20 см, а 7/3 перпендикуляр, который соединяет основания, равен см.

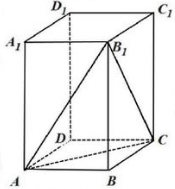
В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ рёбра DA, DC и диагональ CA₁ равны соответственно 6, 5 и √65. Найдите площадь поверхности параллелепипеда ABCDA₁B₁C₁D₁.

Ребро правильного тетраэдра DABC равно a. Постройте сечение тетраэдра, проходящее через середину ребра DA параллельно плоскости DBC, и найдите площадь этого сечения.

Сторона основания правильной треугольной призмы ABCA1B1C1 равна 8, а высота этой призмы равна 6√3. Найдите объём призмы ABCA1B1C1.? Помогите пожалуйста

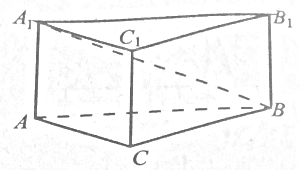
Найдите объём многогранника, вершинами которого являются точки A, B, C, D, A1, B1 прямоугольного параллелепипеда ABCDA1B1C1D1, у которого AB = 7, AD = 4, AA1 = 6.

Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен √3, а высота равна 2.

Образующая конуса равна 5 см, высота 4 см. Найти площадь поверхности и объем.

В сосуде, имеющем форму конуса, уровень жидкости достигает 1/2 высоты. Объём жидкости равен 70 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?

Площадь боковой поверхности треугольной призмы равна 24. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсечённой треугольной призмы.

Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсечённой треугольной призмы равна 43. Найдите площадь боковой поверхности исходной призмы

Найдите площадь боковой поверхности призмы, в основании которой лежит ромб со стороной 11, если высота призмы равна 4,4.

В правильной четырехугольной призме S_пп = 40 см², S_бп = 32 см². Вычислите объем призмы.

Боковое ребро правильной 4–угольной пирамиды равно 6см , высота пирамиды 2см . Найдите сторону основания пирамиды

Найдите объем правильной треугольной призмы со стороной 4см , если известно , что высота этой призмы равна высоте основания

Найдите высоту правильной четырёхугольной усечённой пирамиды, если стороны её основания равны 6 см и 3 см, а боковая поверхность равновелика сумме оснований.

Вычислить площадь боковой поверхности цилиндра, высота которого равна 14 см, а радиус основания 4 см.

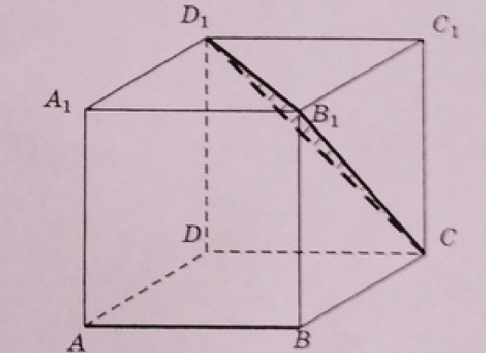
11. В кубе A...D1 найдите угол между прямой AB и плоскостью CB1D1

Из точки Q к плоскости α проведены такие равные наклонные QA и QB, что угол между ними равен 60°, а угол между их проекциями на плоскость α составляет 90°. Найдите угол, который образует наклонная QA с плоскостью α .

В правильной треугольной призме ABCA1B1C1 известно, что AB = AA1. Найдите угол между прямыми A1B и C1C. Ответ дайте в градусах.

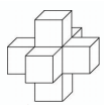
Найдите площадь поверхности пространственного креста, изображенного на рисунке и составленного из единичных кубов. (Л8)

Найдите угол AD2E многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.

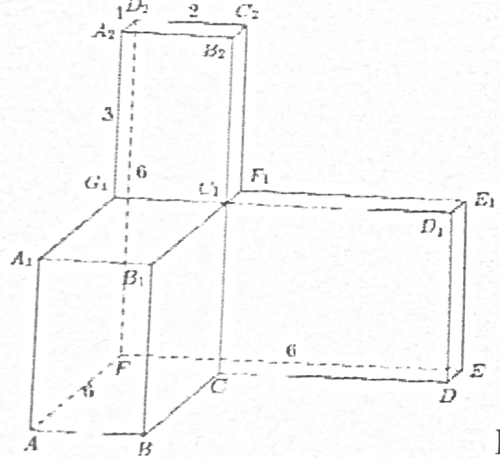
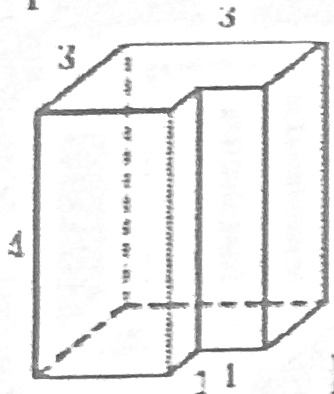
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые)

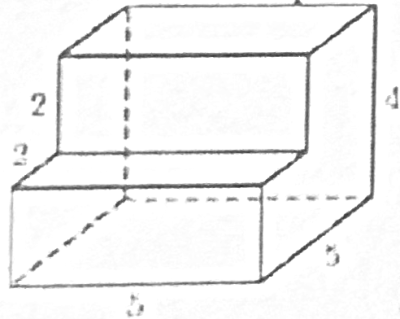
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

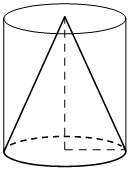
Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 9. Найдите объём цилиндра.

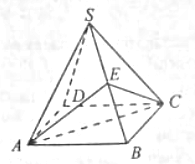
Диагонали грани ABB1A1 правильной треугольной призмы ABCA1B1C1 пересекаются в точке O, ребро основания призмы равно 1, а боковое ребро равно корень из трех. Найдите угол между прямой CO и плоскостью основания призмы

Объём правильной четырёхугольной пирамиды SABCD равен 34. Точка Е — середина ребра SB. Найдите объём тела, полученного после отсечения треугольной пирамиды ЕАВС от пирамиды SABCD

Радиус основания цилиндра равен 5, высота — 4. Найдите площадь сечения этого цилиндра плоскостью, параллельной его оси и отстоящей от нее на расстояние 3.

В основании прямой призмы лежит правильный треугольник со стороной, равной 6. Высота ее равна √3/24. Найти объем призмы.

Расстояние от центра основания правильной четырехугольной пирамиды до боковой грани равно 15 см. боковая грань наклонена к плоскости основания под углом 30°. Вычислите длину стороны основания.

Площадь полной поверхности конуса равна 84. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсечённого конуса.

Площадь боковой поверхности правильной треугольной пирамиды SABC равна 72, а площадь полной поверхности пирамиды SMNQ, отсекаемой от первой плоскостью, параллельной основанию и проходящей через середину высоты, равна 24. Найти площадь треугольника АВС.

Во сколько раз увеличится площадь поверхности куба, если все его рёбра увеличились в 4 раза?

Длина стороны правильной четырёхугольной пирамиды равна √3, а угол наклона плоскости боковой грани к плоскости основания равен 60 °. Найдите объём пирамиды.

Объём первого прямого кругового цилиндра равен 54. Второй прямой круговой цилиндр имеет радиус основания в 2 раза меньше, чем первый, а высоту в 2 раза больше, чем первый. Найдите объём второго цилиндра.