Задача 35309 11. В кубе A...D1 найдите угол между...
Условие
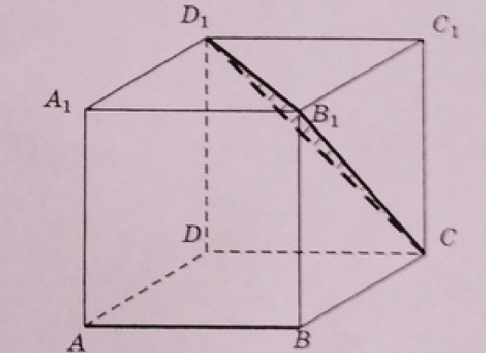
математика 10-11 класс
12914
Все решения
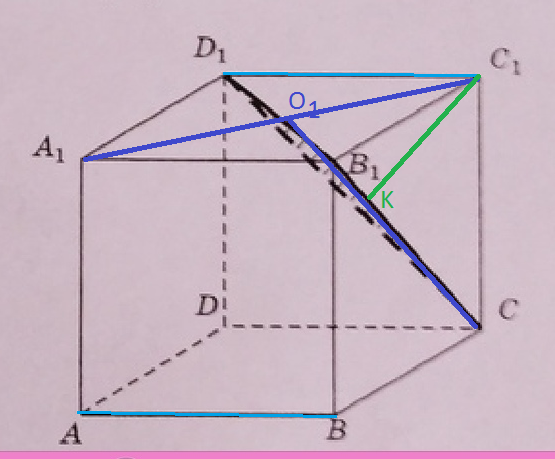
Угол между C1D1 и пл. СВ_(1)D_(1) равен углу между AB и пл. СВ_(1)D_(1)
CO_(1)- высота равнобедренного треугольника СВ_(1)D_(1)
C_(1)K ⊥ CO_(1)
CК – высота прямоугольного треугольника CO_(1)C_(1)
D_(1)К – проекция C1D1 на пл. АВ1С
Из прямоугольного треугольникаCO_(1)C_(1)
CC_(1)=1
C_(1)О_(1)=(1/2)A_(1)C_(1)=√2/2
(CO_(1))^2=1^2+(√2/2)^2=6/4
CO_(1)=√6/2
Из формул площади прямоугольного треугольника находим высоту, проведенную к гипотенузе
C_(1)О_(1)·CC_(1)=CO_(1)·D_(1)К ⇒
CK=(1·√2/2)/(√6/2)=1/√3
sin ∠ C_(1)D_(1)K=D_(1)К/C1D1=1/√3 ⇒
∠ C_(1)D_(1)K= arcsin(1/√3)