Задача 9505 Площадь боковой поверхности треугольной...
Условие
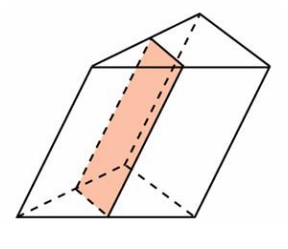
Решение
Таким образом, площадь боковой поверхности отсечённой призмы будет в два раза меньше, чем у исходной.
Высота у призм общая. Указанная плоскость разрезает две соседние боковые грани пополам.
Рассмотрим третью грань (параллельную плоскости сечения) – её площадь поверхности также в два раза меньше, так как средняя линия треугольника в два раза меньше параллельной ей стороны треугольника.
Учитывая, что высота остаётся неизменной (общая для обеих призм), можем сделать вывод, что площадь боковой поверхности (сумма площадей всех трёх граней) отсечённой призмы будет в два раза меньше.
То есть площадь боковой поверхности отсечённой треугольной призмы равна 24:2=12
Ответ: 12
