О категории
Практика (15)
Наблюдатель, находящийся на высоте h м над поверхностью земли, видит линию горизонта на расстоянии l км, которое можно найти по формуле [m] l = \sqrt{\frac{Rh}{500}} [/m], где R = 6400 км — радиус Земли.
Человек, стоящий на пляже, видит горизонт на расстоянии 4,8 километра. К пляжу ве- дёт лестница, каждая ступенька которой имеет высоту 10 см. На сколько ступенек ему нужно подняться, чтобы он увидел горизонт на расстоянии 6,4 километра?
Автомобиль разгоняется на прямолинейном участке шоссе с постоянным ускорением а км/ч^2. Скорость вычисляется по формуле v = sqrt(2la) , где — l пройденный автомобилем путь. Найдите путь, который проехал автомобиль с ускорением а=3500 км/ч^2, если он развил скорость 70 км/ч. Ответ выразите в км/ч^2.
Для обогрева помещения, температура в котором поддерживается на уровне Т_(п) = 25 °С, через радиатор отопления пропускают горячую воду. Расход проходящей через трубу радиатора воды m = 0,5 кг/с. Проходя по трубе расстояние x, вода охлаждается от начальной температуры Т_(в) = 85 °С до температуры T, причём [m]x=\alpha \frac{cm}{\gamma} \log_2 \frac{T_{В}-T_{П}}{T-T_{П}}[/m], где c = 4200 Вт*с/(кг* °С) - теплоёмкость воды, γ = 21 Вт/(м*°С) - коэффициент теплообмена, а α =1,4 - постоянная. Найдите, до какой температуры (в градусах Цельсия) охладится вода, если длина трубы радиатора равна 140 м. [в11-10]
Скорость автомобиля v, разгоняющегося с места старта по прямолинейному отрезку пути длиной l км с постоянным ускорением а км/ч^2, вычисляется по формуле v^2=2la. Определите, с какой наименьшей скоростью будет двигаться автомобиль на расстоянии 400 метров от старта, если по конструктивным особенностям автомобиля приобретаемое им ускорение не меньше 8000 км/ч^2. Ответ выразите в км/ч.
Небольшой мячик бросают под острым углом α к плоской горизонтальной поверхности земли. Максимальная высота полета мячика, выраженная в метрах, определяется формулой H = (v0^2/4g)(1-cos2α), где v0 = 20 м/c - начальная скорость мячика, а g - ускорение свободного падения(считайте g = 10 м/c^2). При каком значении угла α(в градусах) мячик пролетит над стеной высотой 4 м на расстоянии 1 м?
Мяч бросили под углом α к плоской горизонтальной поверхности земли. Время полёта мяча (в секундах) определяется по формуле t=(2*v0*sin α)/g. При каком значении угла α (в градусах) время полета составит 3,2 секунды, если мяч бросают с начальной скоростью v0 = 16 м/с? Считайте, что ускорение свободного падения g = 10 м/с^2.
Груз массой 0,16 кг колеблется на пружине. Его скорость v (в м/с) меняется по закону [b]v = v_(0)cos(2Pit)/T[/b], где t— время с момента начала наблюдения в секундах, T = 2 с - период колебаний, v_(0) = 1,5 м/с. Кинетическая энергия E(в Дж) груза вычисляется по формуле [b]E = mv^2/2[/b] где m - масса груза (в кг), v — скорость груза (в м/с). Найдите кинетическую энергию груза через 20 секунд после начала наблюдения. Ответ дайте в джоулях.
Пользуясь формулой для нахождения объема стенок трубы - V=πh(R^2-r^2),
найдите массу чугунной трубы длинной 3метра, если внутренний диаметр трубы 75мм, толщина 5мм и масса 7.2грамма/1см. куб.
Специализированное агентство намерено ввести рейтинг новостных интернет-изданий на основе показателей информативности In, оперативности Op, объективности Tr публикаций, а также качества сайта Q. Каждый отдельный показатель — целое число от -4 до 4. Составители рейтинга считают, что информативность ценится вшестеро, объективность впятеро, а оперативность публикаций вдвое дороже, чем качество сайта. Таким образом, формула приняла вид
[block] [b]R = (6In+2Op+5Tr+Q)/(A)[/b][/block]
Если по всем четырём показателям какое-то издание получило одну и ту же оценку, то рейтинг должен совпадать с этой оценкой. Найдите число А, при котором это условие будет выполняться.
Автомобиль, движущийся в начальный момент времени со скоростью v0 = 20 м/с, начал торможение с постоянным ускорением a = 5 м/c^2. За t секунд после начала торможения он прошёл путь S = v0t-at^2/2 (м). Определите время, прошедшее от момента начала торможения, если известно, что за это время автомобиль проехал 30 метров. Ответ выразите в секундах.
К источнику с ЭДС E=155 В и внутренним сопротивлением г = 0,5 Ом хотят подключить нагрузку с сопротивлением R Ом. Напряжение на этой нагрузке, выражаемое в вольтах, даётся формулой U = ER/(R+r). При каком сопротивлении нагрузки напряжение на ней будет 150 В? Ответ выразите в омах.
К дну высокого цилиндрического резервуара приварена трубка с краном. После открытия крана вода начинает вытекать из резервуара, при этом высота столба воды (в метрах) меняется по закону H(t) = H_(0) - sqrt(2gH_(0))kt + (g/2)k^2t^2 где t — время в секундах, прошедшее с момента открытия крана, H_(0) = 5 м — начальная высота столба воды, k = 1/800 отношение площадей сечений трубки и резервуара, a g = 10 м/с^2 — ускорение свободного падения. Через сколько секунд после открытия крана в резервуаре останется четверть первоначального объёма воды?
Футболист послал мяч вертикально вверх. Пока мяч не упал, высота, на которой он находится, описывается формулой - 5t^2 + 16t + 1 (h — высота в метрах, t — время в секундах, прошедшее с момента удара). Найдите, сколько секунд мяч находился на высоте не менее 4 метров.
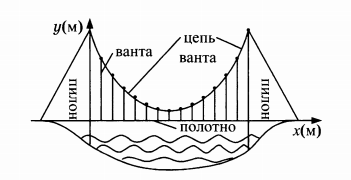
На рисунке изображена схема вантового моста. Вертикальные пилоны связаны провисающей цепью. Тросы, которые свисают с цепи и поддерживают полотно моста, называются вантами. Введём систему координат: ось Оу направим вертикально вдоль одного из пилонов, а ось Ох направим вдоль полотна моста, как показано на рисунке. В этой системе координат линия, по которой провисает цепь моста, имеет уравнение у = 0,0021х^2 - 0,47x + 31, где x и у измеряются в метрах. Найдите длину ванты, расположенной в 70 метрах от пилона. Ответ дайте в метрах.
Расстояние (в км) от наблюдателя, находящегося на небольшой высоте h (в м) от поверхности Земли, до наблюдаемой им линии горизонта вычисляется по формуле: l = sqrt(R·h/500) = 6400 км — радиус Земли. На какой высоте (в м) находится наблюдатель, если l = 8 км?
