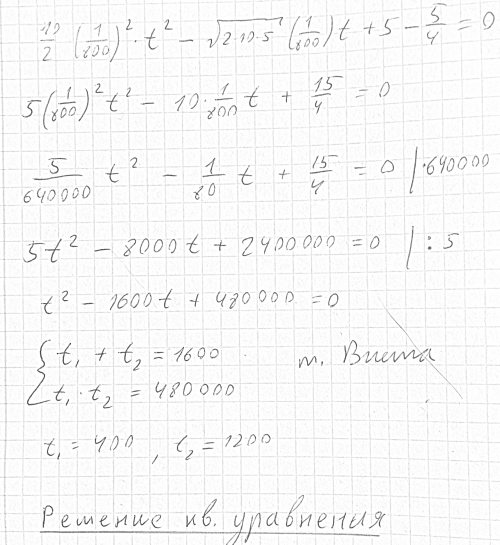К дну высокого цилиндрического резервуара приварена трубка с краном. После открытия крана вода начинает вытекать из резервуара, при этом высота столба воды (в метрах) меняется по закону H(t) = H0 – √2gH0kt + (g/2)k2t2 где t — время в секундах, прошедшее с момента открытия крана, H0 = 5 м — начальная высота столба воды, k = 1/800 отношение площадей сечений трубки и резервуара, a g = 10 м/с2 — ускорение свободного падения. Через сколько секунд после открытия крана в резервуаре останется четверть первоначального объёма воды?
математика 10-11 класс
35985
Объем цилиндра первоначальный V1 = πr2H0
Объем цилиндра ЧЕТВЕРТЬ первоначального V1/4 = πr2H
Откуда H = V1 / 4πr2 = πr2H0 / 4πr2 = H0/4 = 5/4, теперь можем составлять наше уравнение
5/4 = 5 – √2·10·5 · (1/800) · t + (10/2)·(1/800)2·t2
Все что нужно сделать – решить квадратное уравнение, решив которое, мы получаем 2 корня 400 и 1200, первый корень 400 записываем в ответ
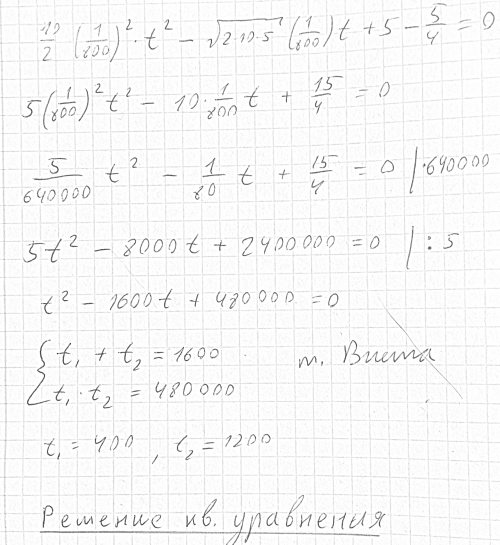
Ответ: 400
Обсуждения
Вопросы к решению (8)
Обратите внимание! Данный функционал устарел, для обсуждения решений используйте функционал, вызываемый кнопкой «Обсуждения»
Лично мне все понятно, может напишите что именно вызывает у Вас вопрос
куда делось t после (1/800) в последнем равенстве?
Да, вы правы, там должно быть t, исправил эту ошибку
У нас получилось квадратное уравнение, график которого парабола, я думаю так как в данном случае вода у нас убывает, логично рассматривать ТОЛЬКО убывающую часть параболы, то есть корень 1200 у нас отпадает, ибо он принадлежит той части параболы, которая возрастает.
покажите решение квадратного уравнения
Если еще будут такие просьбы, прикреплю решение
покажите пожалуйста решение квадратного уравнения
