Задача 20131 Длина стороны правильной четырёхугольной...
Условие
математика 10-11 класс
6128
Решение
Ответ: 1,5
Решение
★
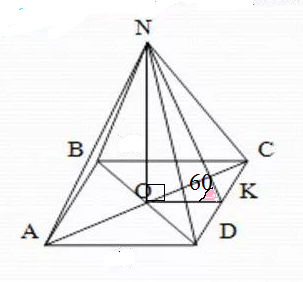
AB=BC=CD=AD=sqrt(3)
ОК=(1/2)AD=sqrt(3)/2
NK⊥CD по теореме от трех перпендикулярах (так как ОК ⊥ СD).
Угол NOK- линейный угол двугранного угла между плоскостью NCD и ABCD, угол наклона боковой грани к плоскости основания
Из прямоугольного треугольника NKO
H(пирамиды)=NO=OK*tg60 градусов=(sqrt(3)/2)*sqrt(3)=3/2
V(пирамиды)=(1/3)S(осн.)*Н=(1/3)*S(квадрата АВСD)*H=
=(1/3)*(sqrt(3))^2*(3/2)=3/2
О т в е т. 3/2=1,5