Задача 34213 ...
Условие
Решение
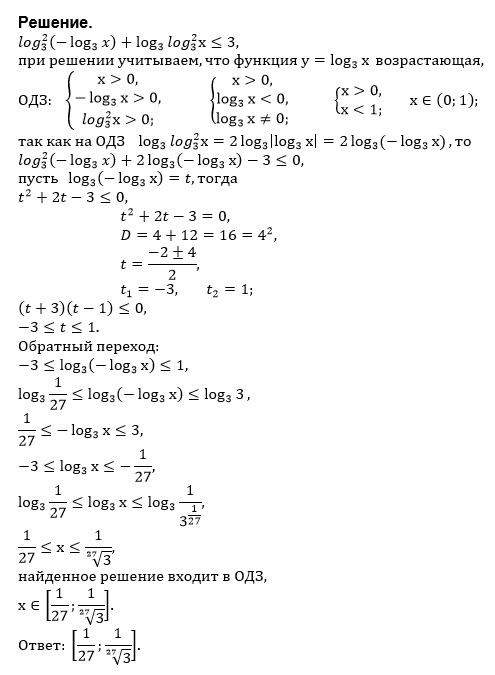
Все решения
(повышенной трудности)
ОДЗ:
{x>0
{- log_(3)x > 0 ⇒ log_(3)x < 0 ⇒
[b] 0 < x < 1[/b]
По свойству логарифма степени
log_(3)t^2=2log_(3)|t|
t=log_(3)x
Так как согласно ОДЗ:
log_(3)x < 0,
| log_(3)x| = - log_(3)x
поэтому
log_(3)log^2_(3)x=log_(3)(log_(3)x)^2=2log_(3)|log_(3)x|=
=2log_(3)(-log_(3)x)
Неравенство принимает вид
log^2_(3)(-log_(3)x) +2log_(3)(-log_(3)x) ≤ 3
[b]log^2_(3)(-log_(3)x) +2log_(3)(-log_(3)x) - 3 ≤ 0[/b] ( #)
Квадратное неравенство
D=4+12=16
корни
-3 и 1
Решение квадратного неравенства (#):
[b]-3 ≤ log_(3)(-log_(3)x) ≤ 1[/b]
1=log_(3)3
-3*log_(3)3 ≤ log_(3)(-log_(3)x)≤ 1* log_(3)3
-3*1=-3log_(3)3=log_(3)3^(-3)
[b]log_(3)[/b]3^(-3) ≤ [b]log_(3)[/b](-log_(3)x)≤ [b]log_(3)[/b]3
Логарифмическая функция с основанием 3 возрастающая, большему значению функции соответствует большее значение аргумента
3^(-3) ≤(-log_(3)x)≤ 3
(1/27) ≤ (-log_(3)x)≤ 3
Умножаем на (-1), знак неравенства меняется на противоположный
-3 ≤ log_(3)x ≤ (-1/27)
-3*log_(3)3 ≤ log_(3)x ≤ (-1/27)*log_(3)3
log_(3)3^(-3) ≤ log_(3)x ≤ log_(3)3^(-1/27)
Логарифмическая функция с основанием 3 возрастающая, большему значению функции соответствует большее значение аргумента
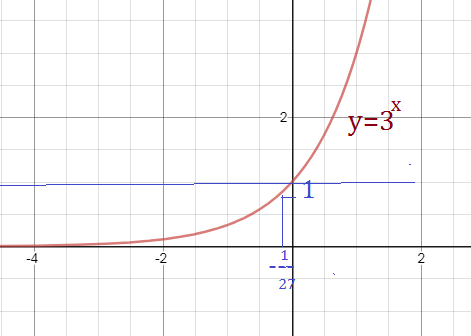
(1/27) ≤ x ≤ 3^(-1/27) входит в ОДЗ, так как
3^(-1/27) < 1 ( см. рис.)
о т в е т. [1/27;3^(-1/27]