Задача 37326 ...
Условие
Решение
2^(x^2)=u
u>0 при любом х
2^(-x)=v
v>0 при любом х
Умножаем и числитель и знаменатель на u >0
(3*u^2+uv)/(4u-v) ≤ 2v
(3*u^2+uv)/(4u-v) - 2v ≤ 0
(3*u^2+uv-8uv+2v^2)/(4u-v) ≤ 0
(3*u^2-7uv+2v^2)/(4u-v) ≤ 0
D=(7v)^2-4*3*2v^2=25v^2
(7v±5v)/6 получим (1/3)v и 2v
(3u-v)*(u-2v)/(4u-v) ≤ 0
Решаем неравенство методом интервалов.
3u-v=0 ⇒ u/v=1/3
u-2v=0 ⇒ u/v=2
4u-v=0 ⇒ u/v=1/4
__-__ (1/4) _+_ [1/3] ___-____ [2] __+__
u/v < 1/4 или 1/3 ≤ u/v ≤ 2
Обратный переход
2^(x^2)/2^(-x) < 1/4 или (1/3) ≤ 2^(x^2)/2^(-x) ≤ 2
2^(x^2+x) < 2^(-2) или 2^(log_(2) (1/3)) ≤ 2^(x^2+x) ≤ 2
Показательная функция с основанием 2 > 1 возрастающая, поэтому
x^2+x < -2 или log_(2)(1/3) ≤ x^2+x ≤ 1
x^2+x+2<0 D=1-4*2<0 неравенство не имеет решений.
log_(2)(1/3) ≤ x^2+x ≤ 1 ⇒
{x^2+x-1 ≤ 0⇒ D=5 ;x ∈ [(-1-sqrt(5))/2; (-1+sqrt(5))/2]
{x^2+x ≥ log_(2)(1/3) - верно при любом х см. рис.
О т в е т. [(-1-sqrt(5))/2; (-1+sqrt(5))/2] 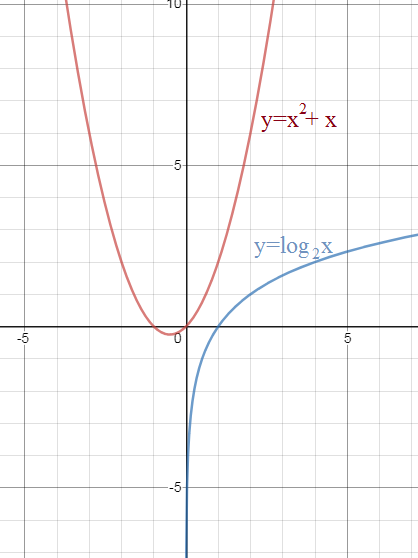
Все решения



