Задача 35264 Решите неравенство...
Условие
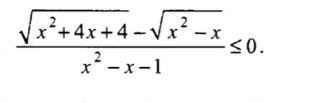
Решение
{x^2+4x+4 ≥ 0 при любом х
{x^2-x ≥ 0 ⇒ x*(x-1) ≥ 0 ⇒ x ≤ 0 или x ≥ 1
Совокупность двух систем
(1)
{sqrt(x^2+4x+4)-sqrt(x^2-x) ≤ 0
{x^2-x-1 >0
или
(2)
{sqrt(x^2+4x+4)-sqrt(x^2-x)≥ 0
{x^2-x-1 <0
x^2-x-1=0
D=1+4=5
x_(1)=(1-sqrt(5))/2 или x_(2)=(1+sqrt(5))/2
sqrt(x^2+4x+4)=sqrt(x^2-x)
x^2+4x+4=x^2-x
5x=-4
x=-4/5
(1)
{x ≥ -4/5
{((1-sqrt(5))/2 ;(1+sqrt(5))/2)
Сравниваем
-4/5 и (1-sqrt(5))/2
Умножаем на 10
-8 и 5-5sqrt(5)
5sqrt(5) и 13
Возводим в квадрат
125 < 169
Значит
-4/5 < (1-sqrt(5))/2
[b]О т в е т. (1)[/b] с учетом ОДЗ:
(1-sqrt(5))/2;0)U(1;(1+sqrt(5))/2)
(2)
{x ≤ -4/5
{x < (1-sqrt(5))/2 или x > (1+sqrt(5))/2
[b]О т в е т (2)[/b]:(- ∞ ; -4/5]
О т в е т. (- ∞ ; -4/5]U (1-sqrt(5))/2;0)U(1;(1+sqrt(5))/2)
Все решения


