Задача 14543 ...
Условие
Решение
{1/x > 0, ⇒ x∈ (0;+ ∞)
{x^2+3x-9 > 0 ⇒ x∈ (- ∞;-1,5-sqrt(10))U(-1,5+sqrt(10);+ ∞)
{x^2+3x+(1/x)-10 > 0 ⇒x^2+3x-10 > (-1/x)
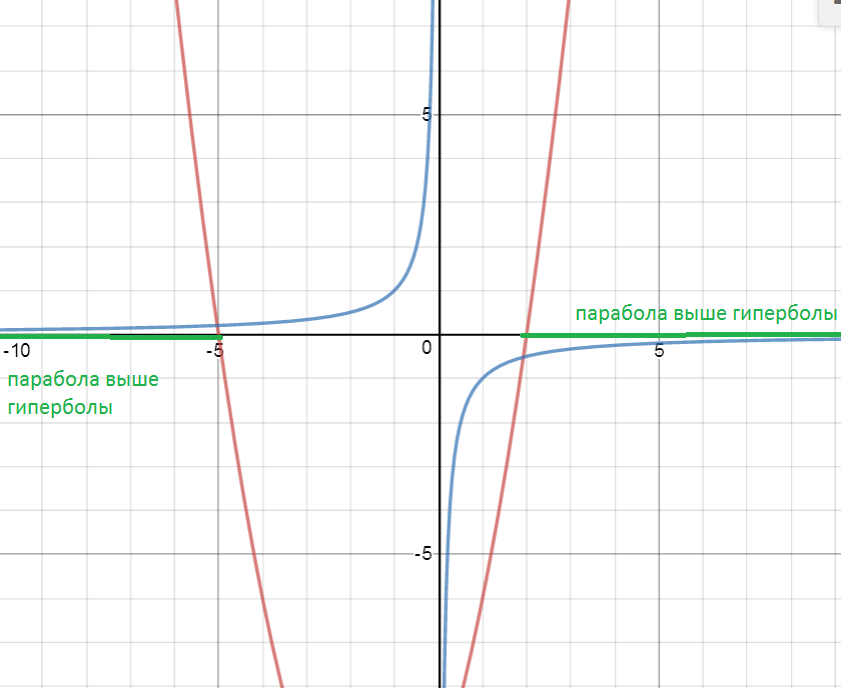
см решение на рисунке
ОДЗ: x∈(b:+бесконечность), b < 2
log_(3)((1/x)*(x^2+3x-9) меньше или равно log_(3)(x2+3x+1/x–10)
Логарифмическая функция с основанием 3 > 1 монотонно возрастает.
(1/х)*(x^2+3x-9) меньше или равно x^2+3x+(1/x) -10;
(1/х)*(x^2+3x-9) -x^2-3x-(1/x)+10 меньше или равно 0;
(1/х)*(x^2+3x-9-1)-(x^2+3x-10) меньше или равно 0;
(x^2+3x-10)*((1/x)-1) меньше или равно 0;
(x-2)(x+5)(1-x)/x меньше или равно 0.
Применяем метод интервалов:
_-___ [-5] __+__ (0) __-__ [1] ___+____ [2] __-_
(-бесконечность;-5]U(0;1]U[2;+бесконечность)
C учетом ОДЗ получаем ответ
[2;+ бесконечность)