Практика (151)
Угол между боковой гранью правильной пирамиды S ABCD и плоскостью основания равен 30°. Найди косинус угла между боковыми гранями пирамиды.
З точки M до площини α проведено похилі MB і MC, які утворюють з площиною кути, що дорівнюють 30°. Знайдіть відстань від точки M до площини α, якщо ∠BMC = 90°, а довжина відрізка BC дорівнює 8 см. (У відповідь записати число).
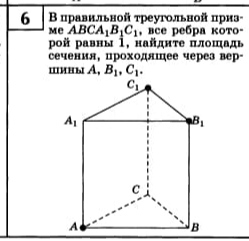
В правильной треугольной призме АВСА1В1С1, все ребра которой равны 1, найдите расстояние от точки А до прямой В1С1
Площадь боковой поверхности правильной усечённой четырёхугольной пирамиды

Задача 11. В правильной четырехугольной призме ABCDA1 B1C1D1 со стороной основания 4 и высотой 7 на ребре АА1 взята точка М так, что АМ=2. На ребре ВВ1 взята точка К так, что
В1К=2. Найдите угол между плоскостью, проходящей через точки D1, M, К и плоскостью СС1D1, расстояние от точки В1 до плоскости D1MK.

Точка М находится на расстоянии 10 см от вершин равнобедренного треугольника АВС (АВ=ВС) и на расстоянии 6 см от его плоскости. Найти стороны треугольника, если ∠ВАС = 30
С дано и рисунком
9 Дано: AB || a_1, AA_1 ⊥ a, BB_1 ⊥ a. Докажите, что AB = A_1B_1.
13 Дано: ABCD — прямоугольник. Найдите расстояние от точки M до (ABCD).
10 Дано: точка O — середина MN. Докажите, что MO = MN_1 = NN_1.
14 Дано: ΔABC — правильный. Найдите расстояние от точки M до плоскости.
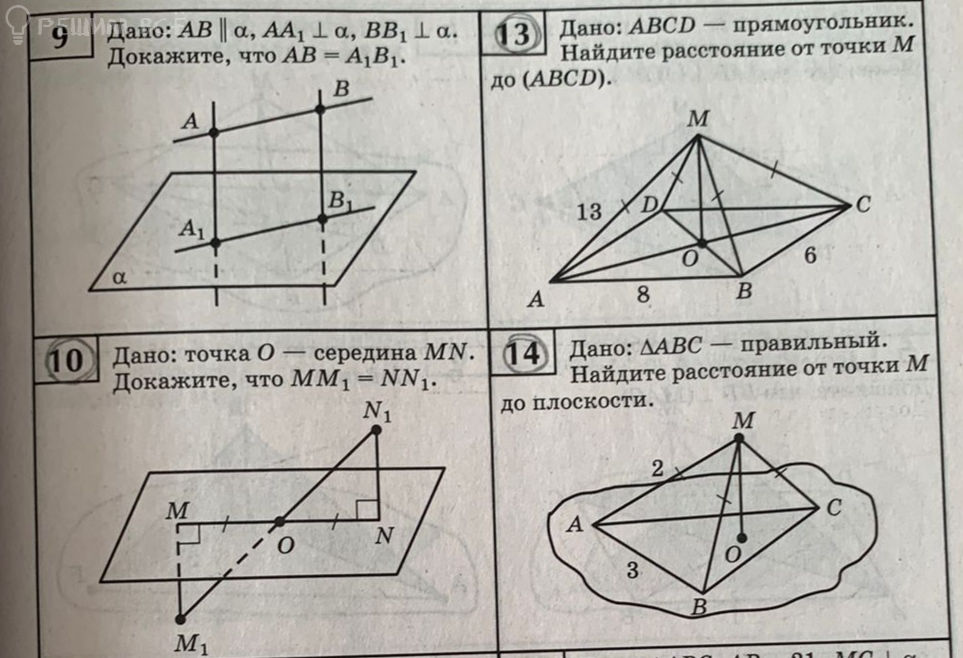
в правильной шестиугольной призме авсдеFа1 в1 с1 д1 е1 F1 известно что АВ=2 АА1=3 Найт расстояние от точки F до палоскости АДС1
З вершини прямого кута C трикутника ABC проведено перпендикуляр
CD до площини трикутника. DB і DA - похилі.
Відомо, що:
CD = 1см;
DB= 3см;
DA= √3 см.
Знайти:
1. довжину невідомої похилої;
2. довжину невідомої проекції;
3. довжину відрізка АВ;
4. довжину медіани CM;
5. довжину відрізка DM;
6. відстань від точки В до площини DCM.
SK перпендикулярно KMN KN=КМ кут KMN=30° SK2 см МN=12см знайти градусну міру двогранового кyта з ребром МN

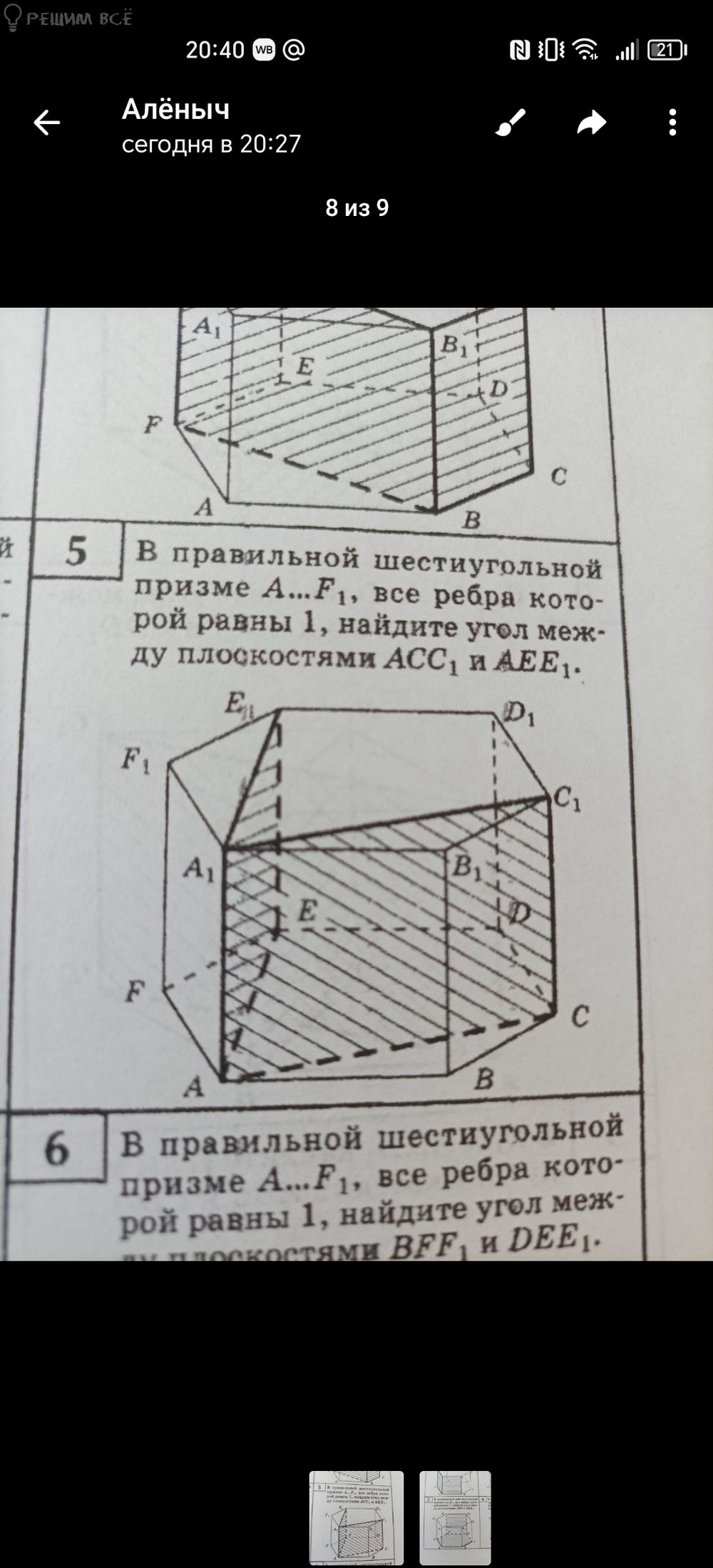
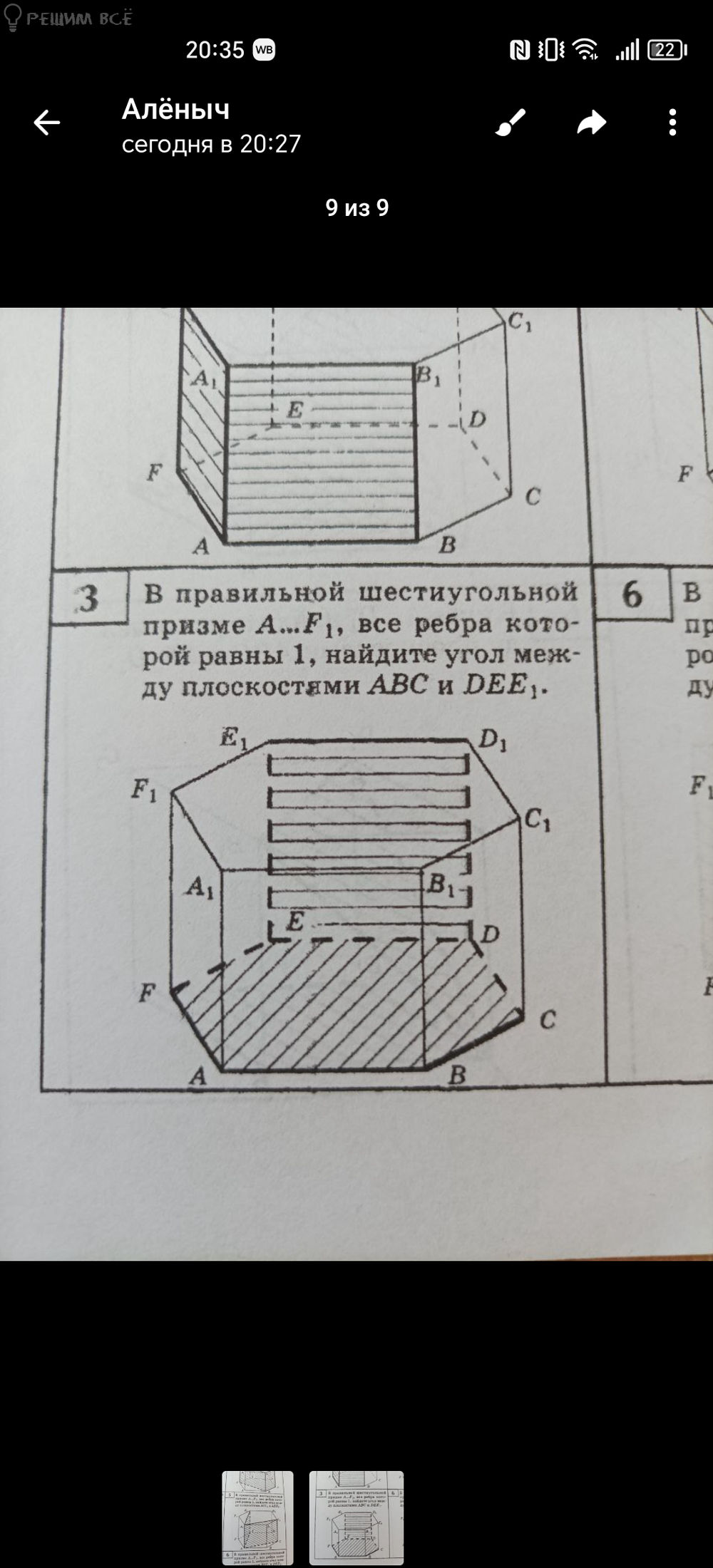
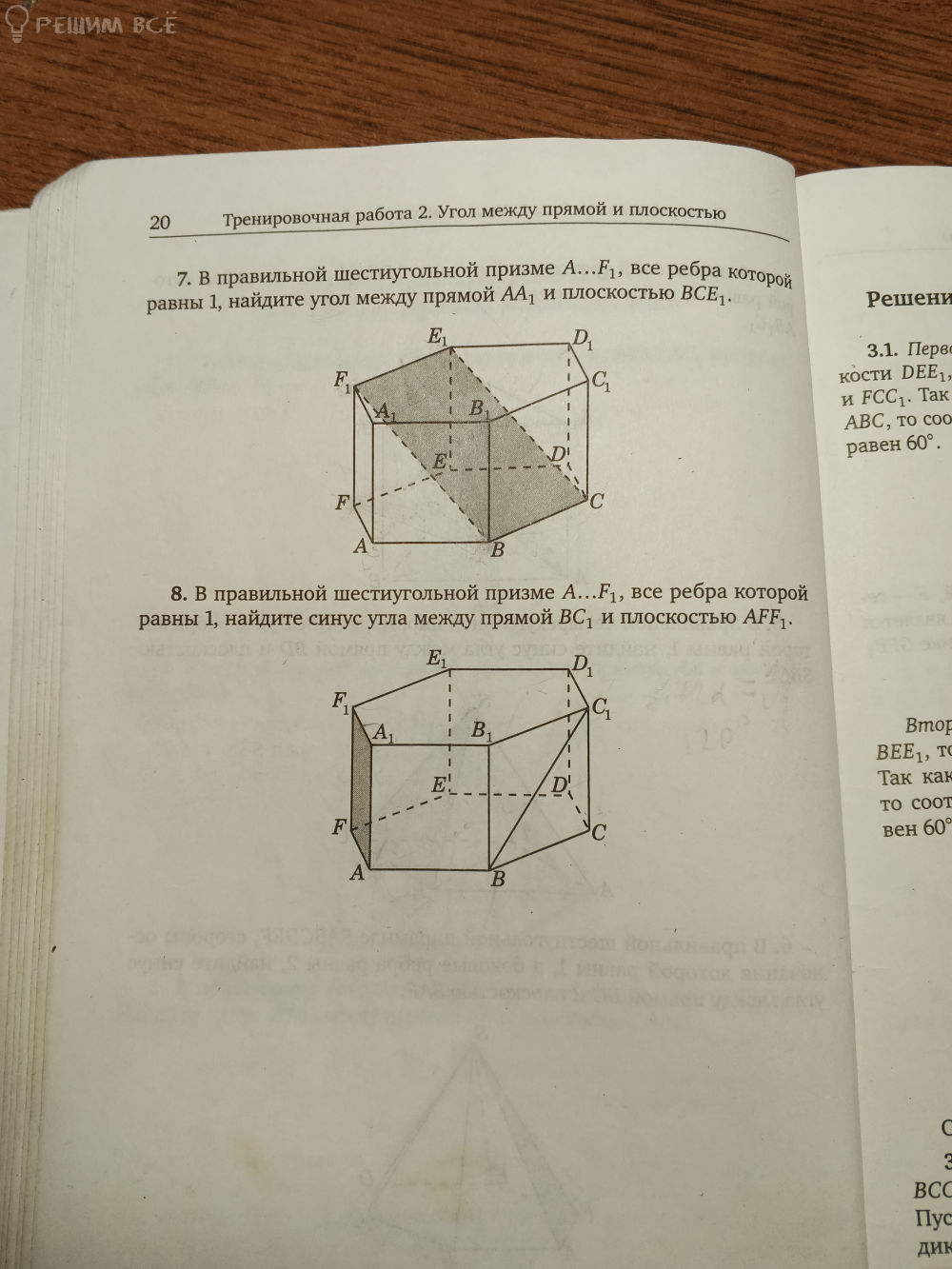
В правильной шестиугольной призме А...F1, все ребра кото- рой равны 1, найдите угол меж- ду плоскостями АВС и DEE.
На ребре SB тетраэдра SABC отметили точку К так, что SK: KB = 3 : 2. Известно, что AB = AC, SB = SC = 13 см, ВС = 24 см. Найдите расстояние между прямыми АК и ВС
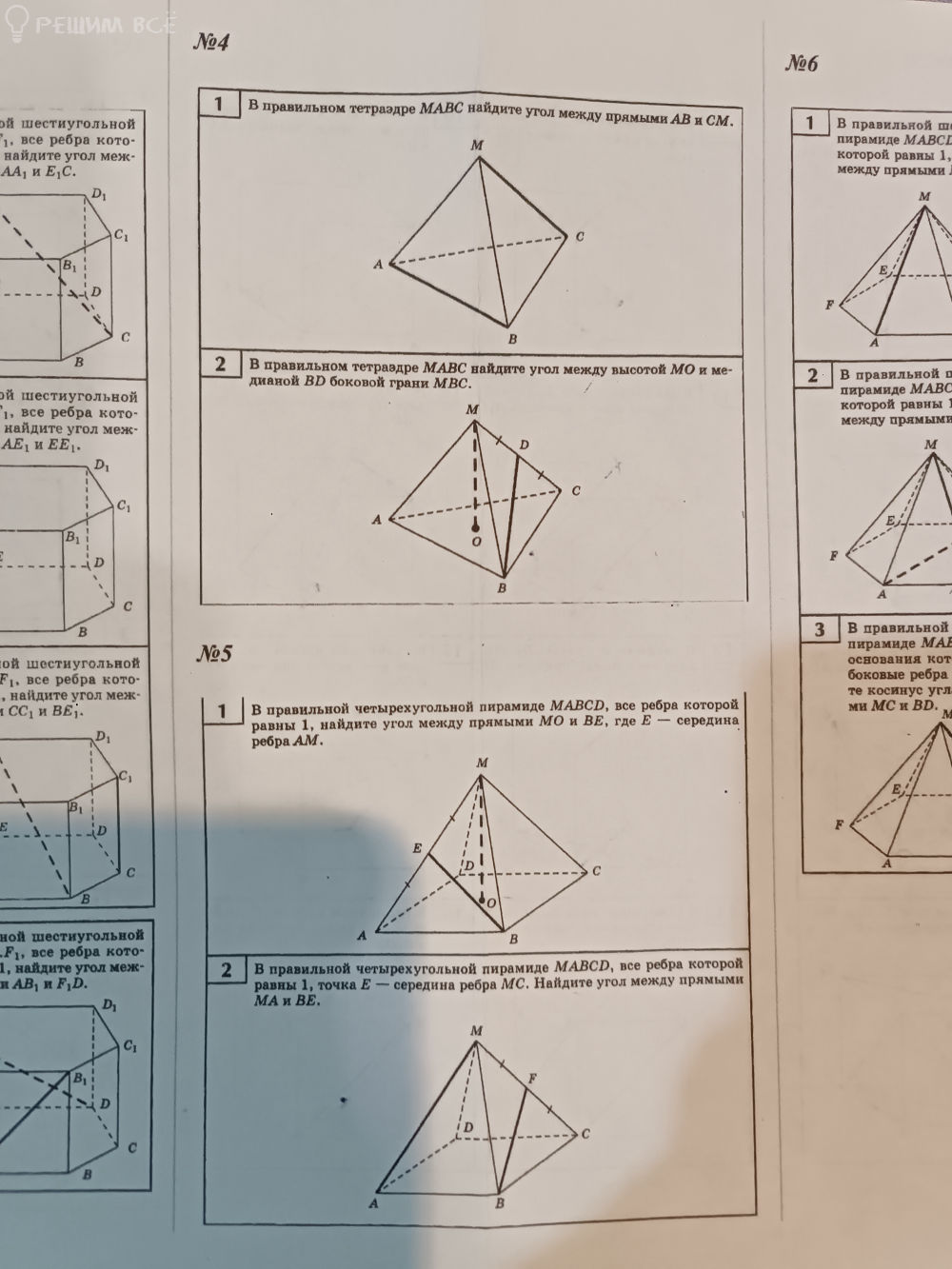
1. В правильном тетраэдре MABC найдите угол между прямыми AB и CM.
2. В правильном тетраэдре MABC найдите угол между высотой MO и медианой BD боковой грани MBC.
1. В правильной четырехугольной пирамиде MABCD, все ребра которой равны 1, найдите угол между прямыми MO и BE, где E - середина ребра AM.
2. В правильной четырехугольной пирамиде MABCD, все ребра которой равны 1, точка Е - середина ребра MC. Найдите угол между прямыми MA и BE.
З вершини прямого кута C трикутника ABC проведено перпендикуляр
CD до площини трикутника. DB і DA - похилі.
Відомо, що:
CD = 1см;DB= 3см;DA=√3см
Знайти:
1. довжину невідомої похилої;
2. довжину невідомої проекції;
3. довжину відрізка АВ;
4. довжину медіани CM;
5. довжину відрізка DM;
6. відстань від точки В до площини DCM
Основание пирамиды - треугольник со сторонами 5,5 и 6 см, а все двугранные углы при сторонах основания равны 60 градусов. Найдите длину высоты пирамиды
Как решить?
Два конуса имеют общую высоту и параллельные основания , радиусы которых равны R и r. Найти радиус окружности , по которой пересекаются поверхности конусов .
ABCDEFA1B1C1D1E1F1 - правильная шестиугольная приз-ма, все ребра которой равны 1. Найдите расстояние между прямыми А1F и AB1
В правильной треугольной призме АВСA1В1С1 точка М - середина ребра АА1 , точка К - середина ребра BB1 . Найдите расстояние от вершины А1 до плоскости CМК, если AA1 = 6, AB = 4

Задача 3. В правильной шестиугольной призме ABCDEFA1B1C1D1 E1 F1 , все рёбра которой равны 1, найдите расстояние от точки А до плоскости BFE1 .

Основанием прямой призмы служит треугольник с катетами 5 и 12 пользуясь площадью её поверхности 120 найти высоту призмы
Допоможіть вирішити задачі
геометрия 10 класс 8 задача!!:( с рисунком, если можете
Основанием пирамиды
SABCD
является прямоугольник
ABCD.
Ребро
SB
перпендикулярно плоскости основания. Перпендикулярно ребру SD через его середину проведена плоскость, пересекающая прямую ВС в точке К. Найдите отрезок
ВК, если АВ = 2 см, ВС = 4 см, SB=6 см
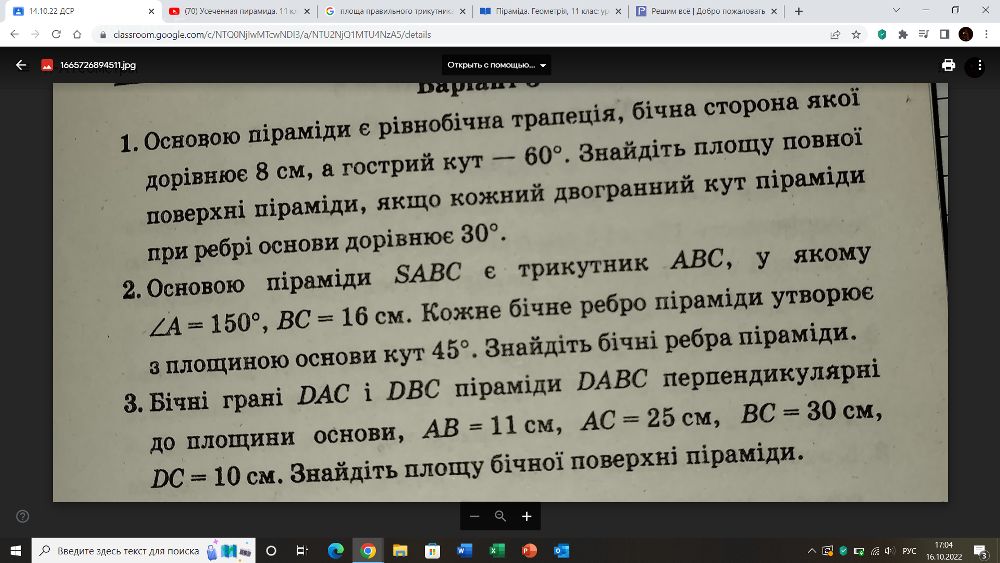
Основою піраміди є правильний трикутник зі стороною 8 см. Одна з бічних граней перпендикулярна до площини основи, а дві інші утворюють з нею кути по 60°. Знайдіть площу бічної поверхні піраміди.
Через сторону нижньої основи і середину протилежного бічного ребра правильної трикутної призми проведено переріз під кутом 45° до площини основи. Знайдіть площу поверхнi призми, якщо площа перерізу 4√3 см².
СР0ЧНО!!!геометрия 10 класс
Основанием пирамиды является квадрат, одна из боковых рёбер перпендикулярна плоскости основания. Плоскость боковой грани, не проходящей через высоту пирамиды наклонена к плоскости основания под углом 45°.Наибольшее боковое ребро 12 см. Найдите высоту пирамиды.
Отрезок AD перпендикулярен к плоскости равнобедренного треугольника ABC. Известно, что AB=AC=6 см, BC=8 см, AD=15 см а) Выполните чертеж по условию задачи. б) Найдите расстояния от концов отрезка AD до прямой BC.
срочно
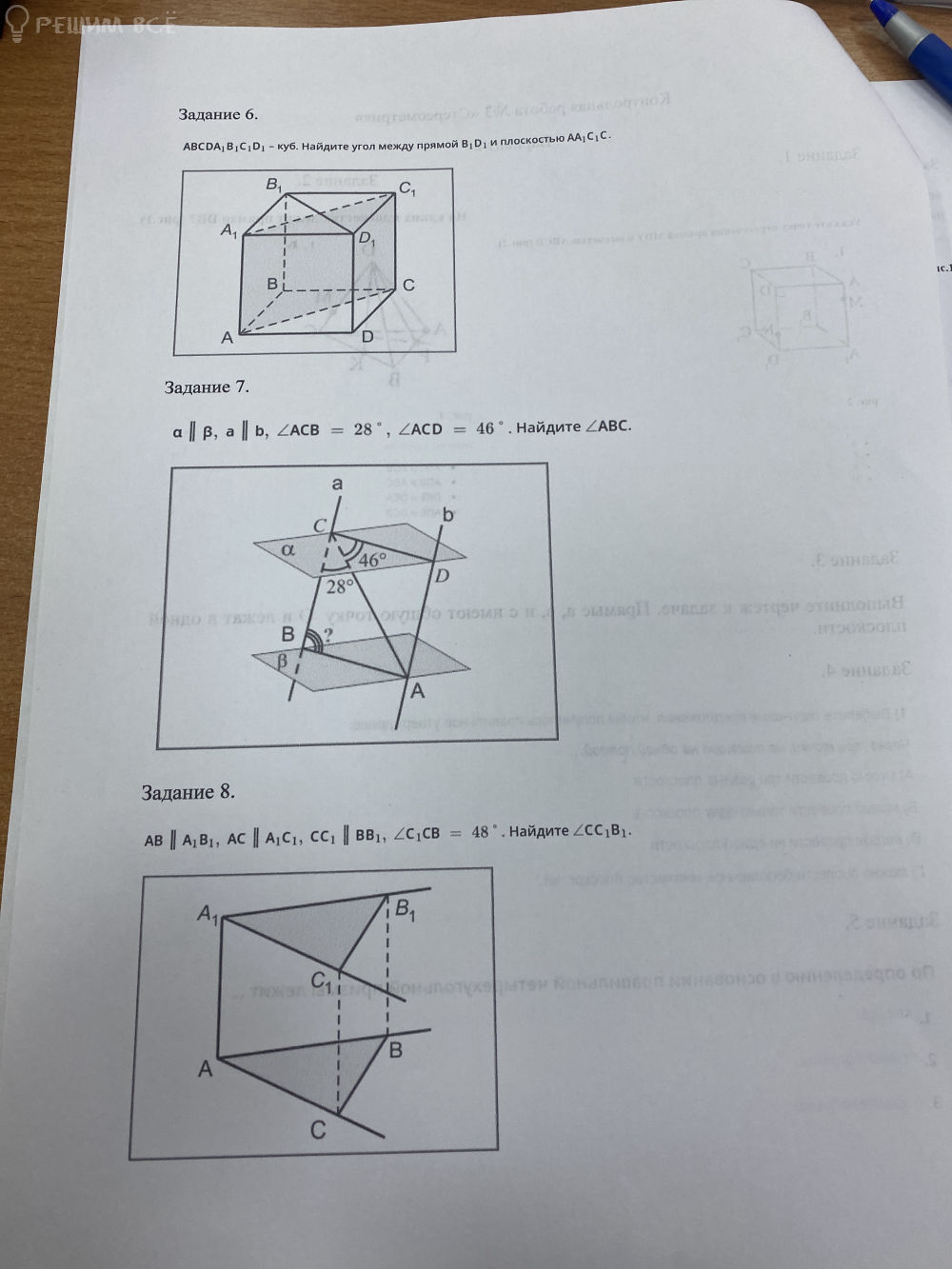
На рисунке изображена прямоугольная треугольная призма высотой 2 единицы. расстояние от точки А' до прямой BC.
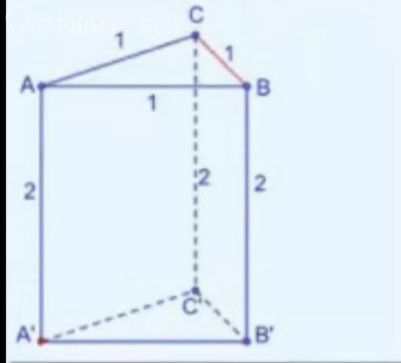
Грани abcda1b1c1d1 равны 1 см. Найдите синус угла между падением BD1 с плоскостью ACB1.
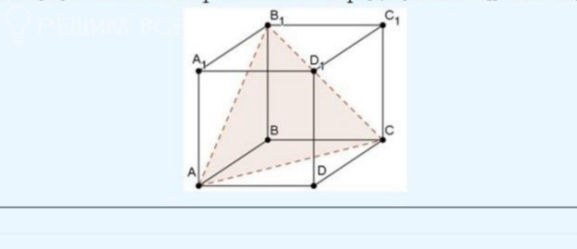
На рисунке угол между прямым шестиугольным празманом 2 единицами CE' и векторами DF.
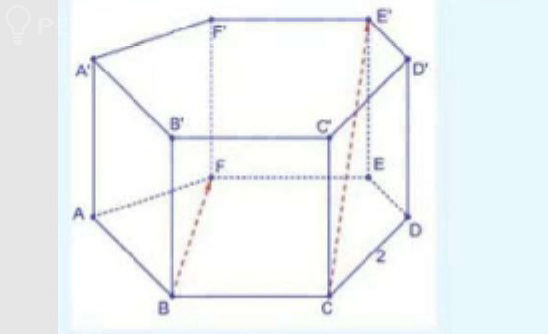
Основою піраміди є ромб, сторона якого дорівнює 24 см і гострий кут дорівнює 30°.
Усі двогранні кути при основі дорівнюють60°.
Обчисли висоту і площу бічної поверхні піраміди.
Висота правильної трикутної піраміди дорівнює 6 см, а кут, який утворює апофема з площиною основи піраміди, дорівнює 30°. Обчисли об'єм піраміди.
Решите задачу по геометрии с правильной треугольной пирамидой

1. Рівнобедрені трикутники ABC і ABD мають спільну основу АВ. Кут між їхніми площинами дорівнює 60°. Знайдіть відрізок CD, якщо ВС= 15 см, BD = 13 см, АВ = 24 см.
Кінці відрізка, довжина якого дорівнює 13 см, належать двом перпендикулярним площинам, а відстані від кінців відрізка до лінії перетину площин дорівнюють 8 см і 5 см. Знайдіть відстань між основами перпендикулярів, проведених із кінців даного відрізка до лінії перетину площин.
Площа трапеції дорівнює 48√3 см2 , а її ортогональна проекція на площину α — рівнобічна трапеція з основами 4 см і 20 см та бічною стороною 10 см. Знайдіть кут між площиною α та площиною даної трапеції.
Диагональ боковой грани правильной
треугольной призмы образует с боковым
ребром угол 60 градусов
. Радиус окружности,
вписанной в основание, равен √3 см.
Определите площадь полной поверхности
призмы.
1. Пользуясь рисунком, где СА и СВ – наклонные к плоскости α, СМ – пер- пендикуляр, АМ = 12 см, МВ = 15 см, указжите верные неравенства: а) ВС < СМ; б) МС < МА; в) СА < СВ; г) МВ > СМ.
2. Основанием прямоугольного параллелепипеда является пря- моугольник с измерениями 2 см и 14 см, а диагональ паралле- лепипеда равна 15 см. Найдите третье измерение параллелепи- педа.
3. Стороны прямоугольника АВСD рав- ны 6 см и 6√3 см. К плоскости прямо- угольника через точку пересечения его диагоналей проведен перпендикуляр РО, равный 6 см. Найдите угол между прямой РС и плоскостью прямоуголь- ника АВСD.

Дан равносторонний треугольник АВС со
стороной 8√3 см. Сторона АС принадлежит
плоскости α, а вершина В этой плоскости не
принадлежит. Основание перпендикуляра,
проведённого из вершины В к плоскости α
удалено от АС на 6√3 см. Под каким углом
наклонён треугольник АВС к плоскости α?
В прямоугольном параллелепипеде ABCDA1B1C1D1 найдите угол между плоскостью АА1Си прямой А1В, если АА1=3, АВ=4, ВС=3
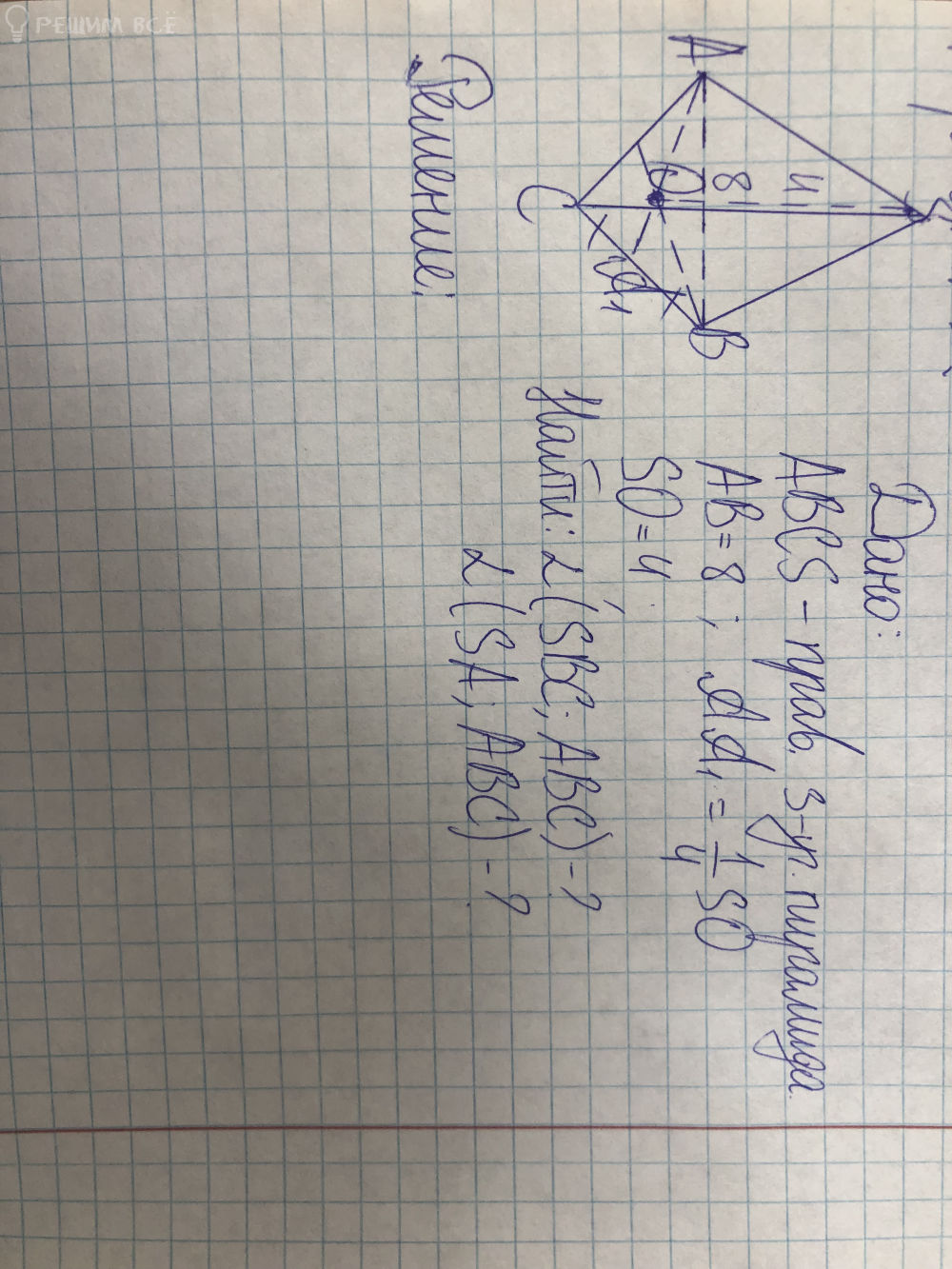
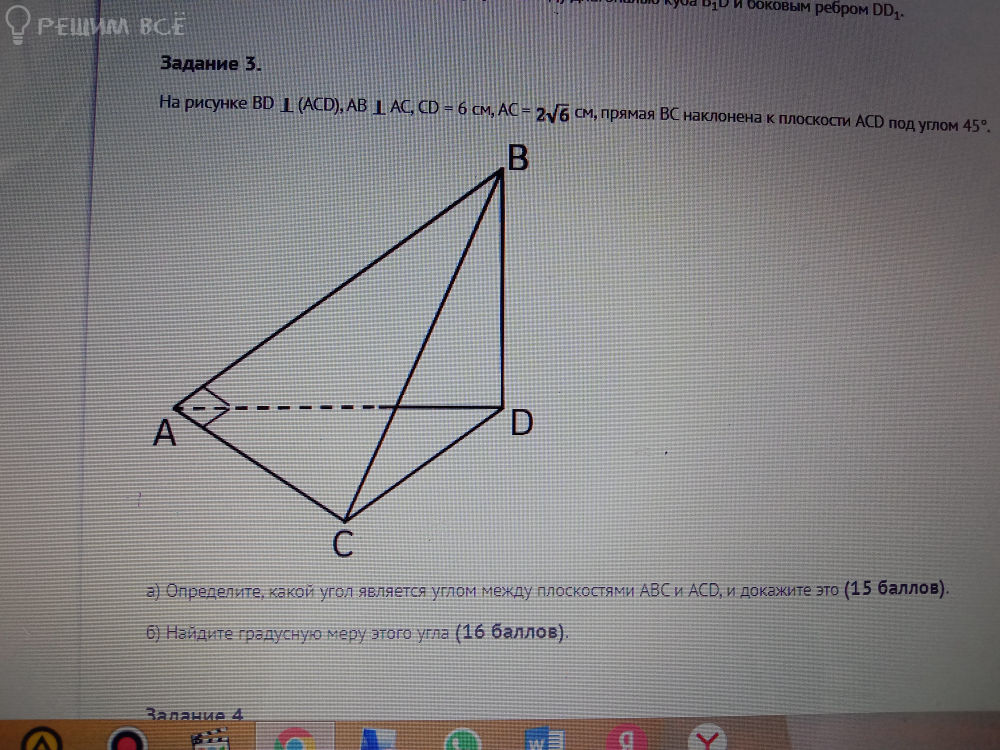
На рисунке BD ⊥ (ACD),AB ⊥ AC=2√6см, прямая BC наклонена к плоскости ACD под углом 45 °
а)определите, какой угол является углом между плоскостями ABC и ACD,и докажите это
Б) найдете градусную меру этого угла
3. В правильной четырехугольной призме ABCDA1B1C1D1 через точки B, D, C1 проведена плоскость, отсекающая от призмы треугольную пирамиду. Площадь сечения призмы плоскостью равна 6. Расстояние от точки С, до плоскости сечения равно 2. Найдите объем призмы
›т всех вершин < ©0 стороной 12 сми ЯНИИ # см от ПЛоСКостИ ' Расстояние от угольника. на расстоянии 6 см от 1е СА и СВ образуют с лы 30° и 45° соответственно, - "ние между точками А и В, если оекциями наклонных равен 30°. оао а [ - ч J‘.

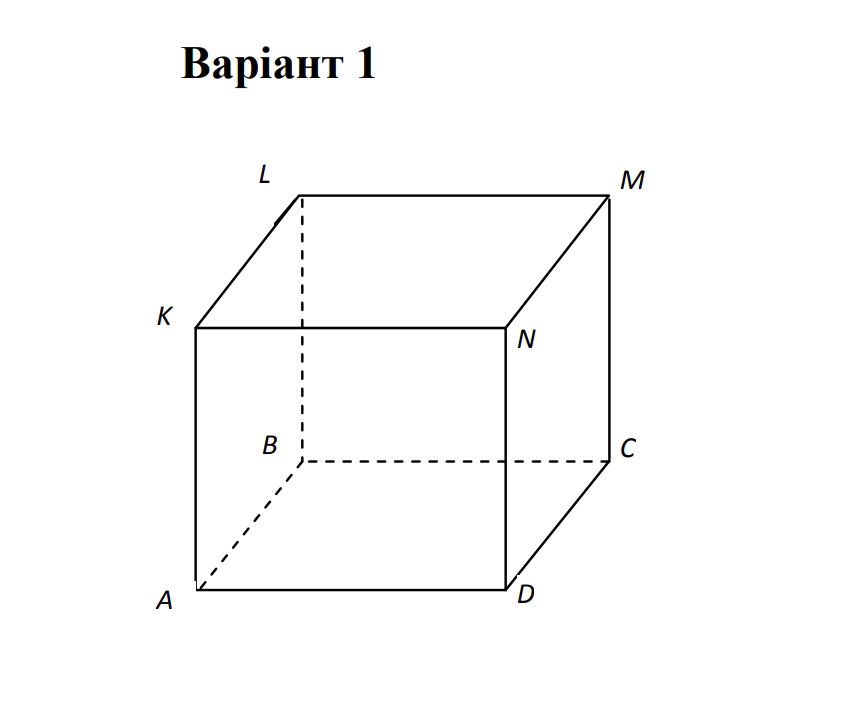
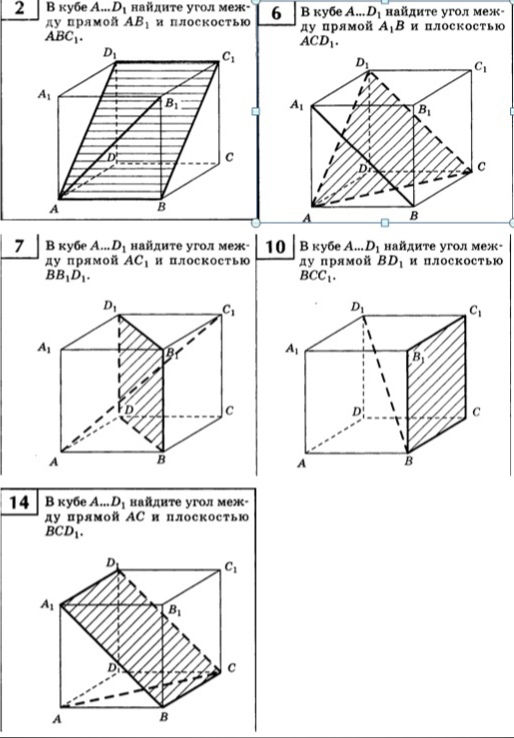
5 В кубе A₁...D₁ найдите угол между прямой AB₁ и плоскостью ABC₁.
6 В кубе A₁...D₁ найдите угол между прямой A₁B и плоскостью ACD₁.
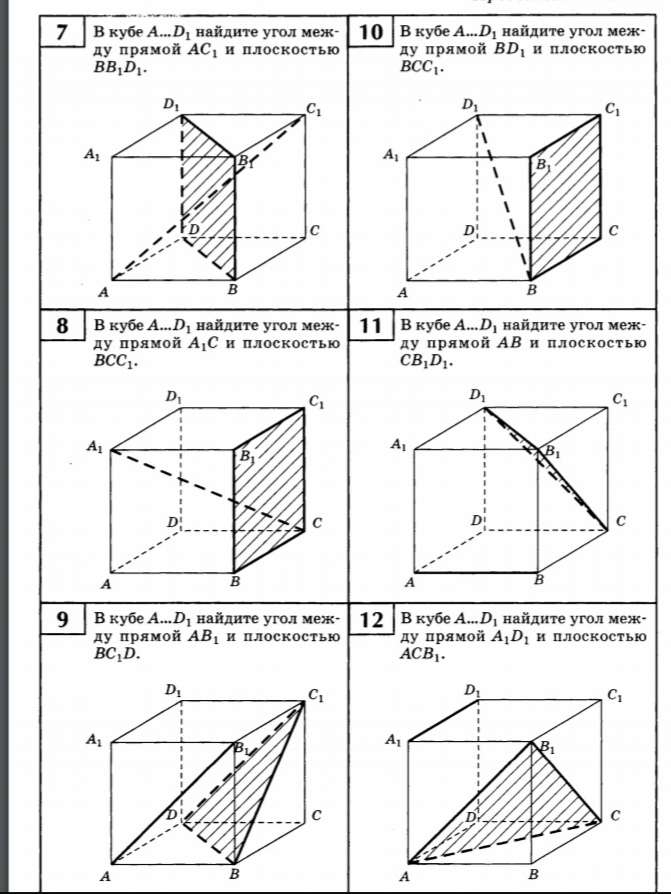
7 В кубе A₁...D₁ найдите угол между прямой AC₁ и плоскостью BB₁D₁.
10 В кубе A₁...D₁ найдите угол между прямой BD₁ и плоскостью BCC₁.
14 В кубе A₁...D₁ найдите угол между прямой AC и плоскостью BCD₁.
Нужно решить
Ребро CD тетраэдра ABCD перпендикулярно к плоскости ABD. Найдите угол между плоскостями ABC И ABD, если AC=BC, ∠ ACB=90 ° и ∠ CAD=30 °
В основании четыругольной пирамилы SABCD лежит прямоуголньки ABCD. Точка M- серелина реьра BC. Известно, что AD=2AB, а SA= SB= SC= AD. Найдите угол между плоскостями SAM и SDM
дан куб ABCDA1B1C1D1 найдите угол между прямой BD и плоскостью ABC1
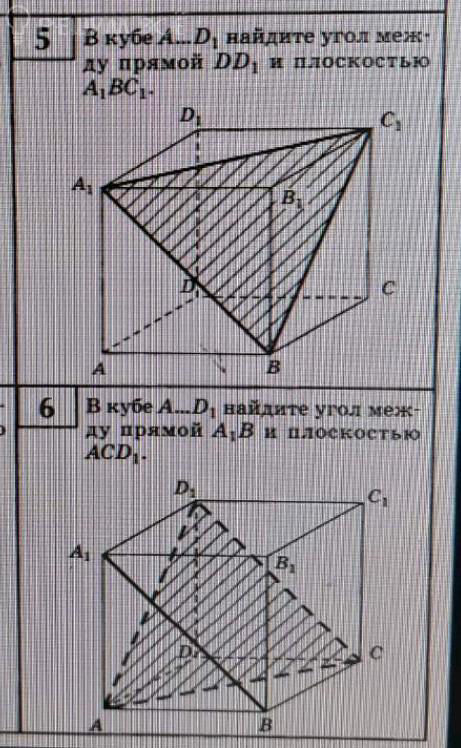
5) в кубе a...d1 найдите угол между прямой dd1 и плоскостью a1bc1
6) в кубе a...d1 найдите угол между прямой a1b и плоскостью acd1
Прямокутник АВСD перегнули по діагоналі ВD так що площини АВD і СВD виявились перпендикулярними . знайти відстань між точками А і С у новому положені якщо АВ=30 см ВD=50 см
АВСД – квадрат. ВР┴ (АВС). Найдите РД, если ВР = 4 и ∟ РСВ = 30 градусов
дан единичный куб ABCDA1B1C1D1. найдите расстояние от точки D до плоскости AB1D1.
Угол между диагональю и гранью прямоугольной призмы с основанием 2 равен 30º. Из приведенных ниже ответов укажите значение (значения), которое может быть равно числовому значению объема призмы.
Дан прямой параллелепипед ABCDA1B1C1D1, в основании - параллелограмм. Показать угол между диагональю B1D прямого параллелепипеда и боковой гранью DD1C1C :
катеты прямоугольного треугольника равны 8 и 7 см, найдите проекцию этого треугольника на плоскость, если плоскость треугольника наклолена на плоскость проекции под углом 30 градусов (если можно, то с условиеи и чертежом)
длины диагоналей трех граней прямоугольного параллелепипеда, имеющих общую вершину, равны sqrt(10), sqrt(17) и 5см,найдите диагональ параллелепипеда (если можно, то с чертежом и условием)
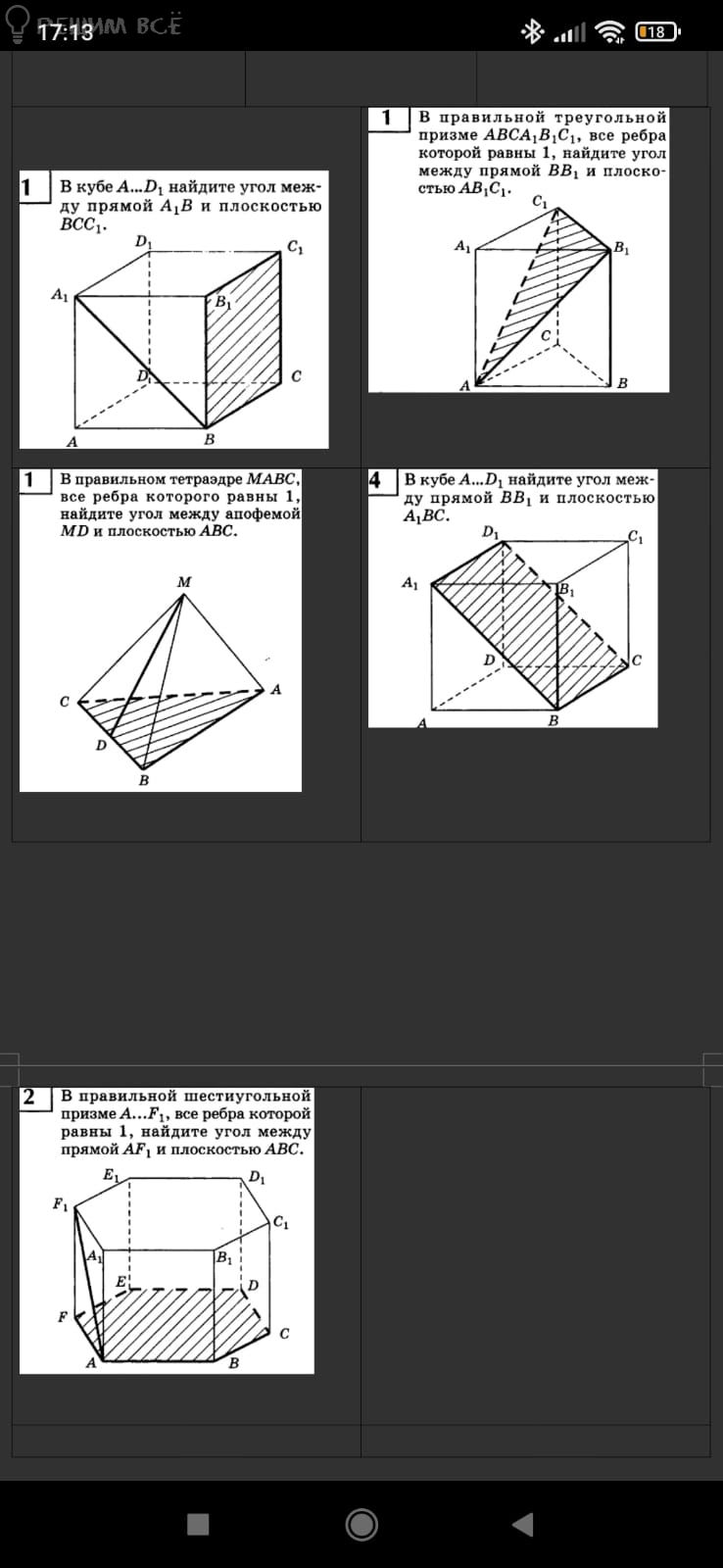
1) в Кубе а.. Д1, найдите угол между прямой А1В и плоскостью ВСС1
1. Знайдіть бічне ребро та апофему шестикутної зрізаної піраміди, якщо сторони основи дорівнюють 8 см і 12 см, а бічне ребро нахилене до площини основи під кутом 600.
В кубе A....D1 найдите угол между прямой и плоскостью AB1 и BCC1
В кубе А...D1 найдите угол между прямой... и плоскостью...
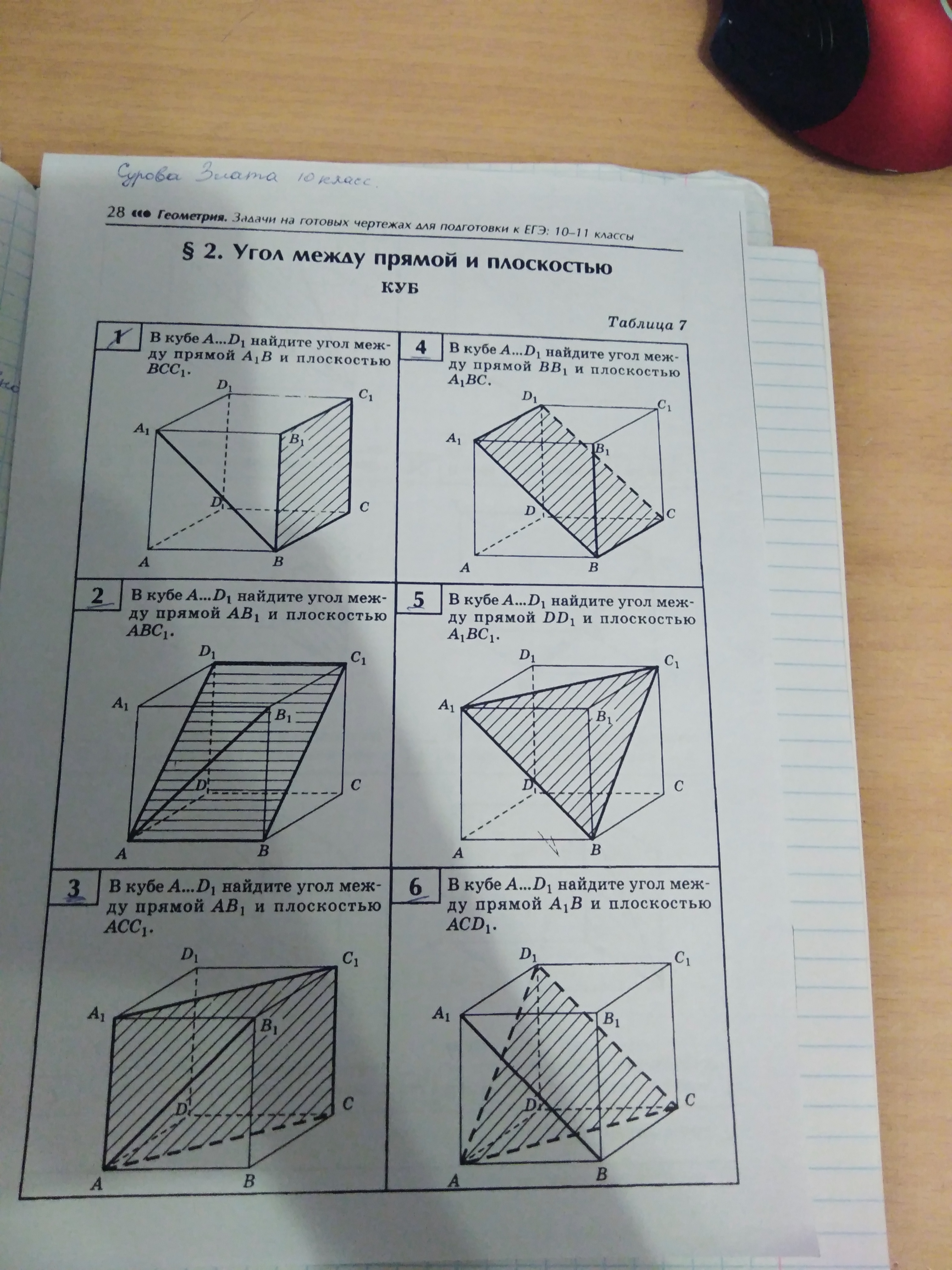
7. В кубе А...D1, найдите угол между прямой АС1, и плоскостью BB1D1
8. В кубе A...D1, найдите угол между прямой А1С и плоскостью BCC1.
9. В кубе А...D1, найдите угол между прямой АВ1, и плоскостью BC1D
10. В кубе А...D1, найдите угол между прямой BD1 и плоскостью ВСС1.
11. В кубе А...D1, найдите угол между прямой АВ и плоскостью СВ1D1.
12. В кубе А...D1, найдите угол между прямой А1D1 и плоскостью АСВ1.
В равнобедренном треугольнике ABC основание AC равно 12см. AB=BC=10см. BP перпендикулярен (ABC), BP=6см. Выполните рисунок.Найдите расстояние от точки P до стороны AC.
решить задачу по геометрии очень нужно

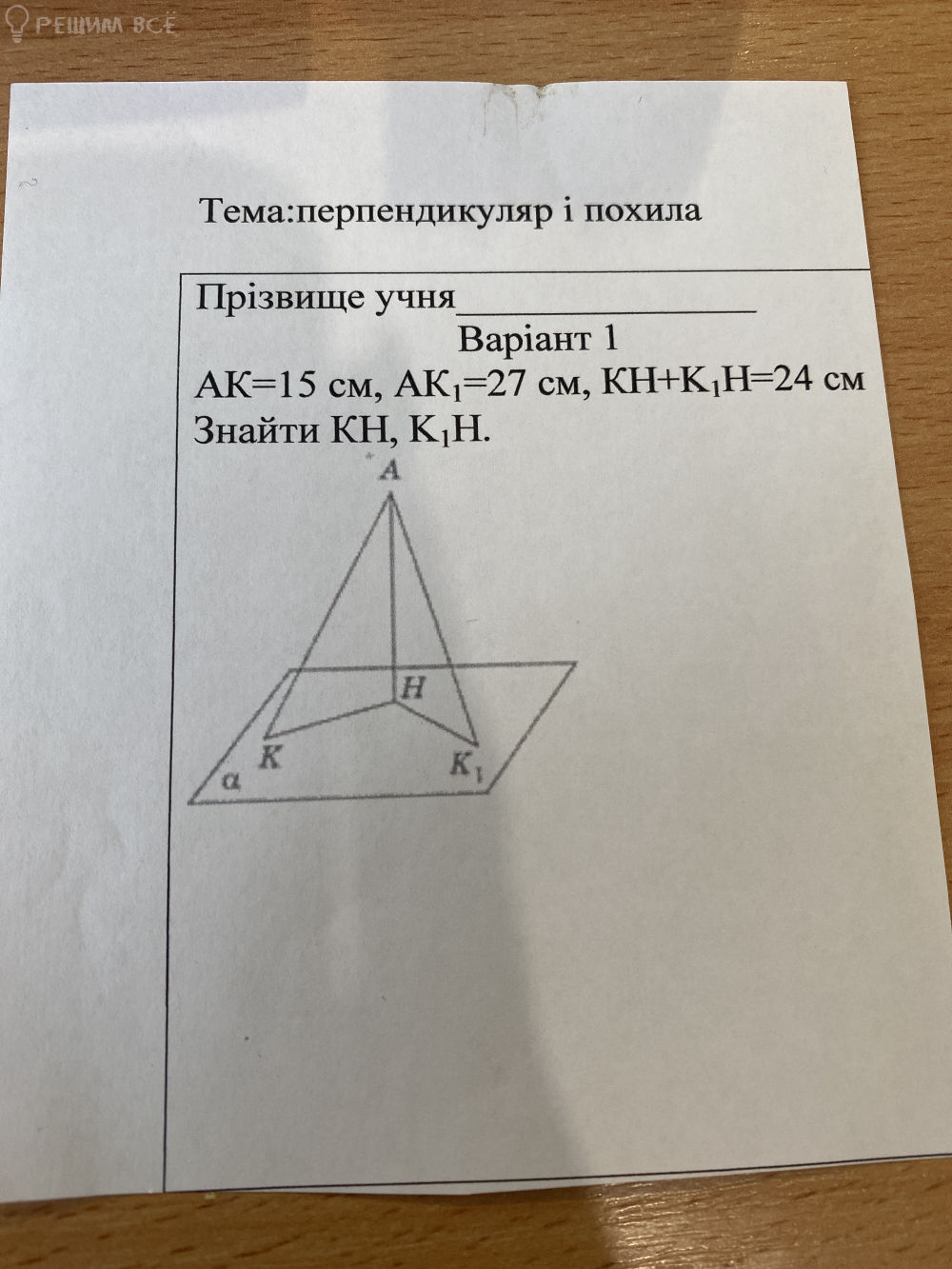
АК=15 см, АК₁=27 см, КН+К₁Н=24 см
Найти КН, К₁Н.
для прямоугольного параллелепипеда ABCDA1B1C1D1, у которого AB=2, AD=2, AA1=1, найдите косинус угла между плоскостями ABC1 и ACD
Для прямоугольного параллелепипеда ABCDA1B1C1D1, у которого AB=2, AD=2, AA1=1, найдите расстояние от вершины A1 до плоскости ABC1
для прямоугольного параллелепипеда ABCDA1B1C1D1, у которого AB=2, AD=2, AA1=1, найдите расстояние от вершины A1 до плоскости ACD1
Дан куб ABCDA1B1C1D1.
На рёбрах B1C1 и C1D1 соответственно отмечены точки N и M так, что B1N:NC1=1:4;C1M:MD1=1:4.
Определи косинус угла α между прямыми BN и CM, если ребро куба равняется 1 ед. изм.
Ответ: cosα=
С подробным решением :
Точка О – центр основания цилиндра. ОО1 – ось цилиндра. ОА = 5 см. На расстоянии 3 см от оси цилиндра проведено сечение АА1В1В, параллельное оси. АА1В1В – квадрат.
а) Вычислите площадь данного сечения б) Площадь осевого сечения цилиндра.
Дан конус. О1 – центр основания конуса, О1О – высота конуса Sосн.= 15см2, Sбок. пов. = 17см2. АОВ – осевое сечение. Найдите площадь треугольника АОВ.
(Sосн. – площадь основания конуса, Sбок.пов. – площадь боковой поверхности конуса.)
Дан усеченный конус. О и О1 – центры оснований. ОО1 = h, ОВ = R, ∠ВВ1О1 = ????. Вычислите площадь боковой поверхности конуса.

Основой пирамиды является прямоугольный треугольник, один из катетов которого равен альфа, а прилегающий к нему угол равен бетта. Каждое боковое ребро пирамиды наклонено к плоскости основания под углом у. Найдите боковое ребро пирамиды.
Боковые рёбра треугольной пирамиды взаимно перпендикулярны и равны 5 см, 6 см, 7 см. Вычислите длины сторон её основания.
Сторона основания правильной треугольной пирамиды равна 12 см, а высота-2 см. Найдите апофему пирамиды. Подробно с объяснениями.
найдите косинус двугранного угла, образованного соседними боковыми гранями правильной четырехугольной пирамиды, все ребра которой равны 1
Тангенс угла между боковыми гранями правильной треугольной пирамиды равен 2 корня из 2. Найдите градусную меру плоского угла при вершине пирамиды.
Дан куб ABCDA B1 C1 D1 . Найдите угол междупрямыми А1В и АС1. Ответ дайте в градусах.
В основании пирамиды лежит прямоугольный треугольник с катетами 6 и 8. Объём пирамиды равен 40. Все боковые рёбра наклонены к плоскости основания под одинаковым углом, Найдите этот угол.
Выберите один ответ:
a. 65°
b. 45°
c. 75°
d. 30°
e. 60°
площадь боковой поверхности цилиндра равна 24п а радиус цилиндра 4 найти объем цилиндра
Дан куб ABCDA1B1C1D1.
На рёбрах B1A1 и A1D1 соответственно находятся точки N и M так, что B1N:NA1=1:1;A1M:MD1=1:1.
Определи косинус угла α между прямыми BN и AM, если ребро куба равняется 1 ед. изм.
Даны параллелограмм ABCD и не пересекающая его плоскость . Через вершины параллелограмма A,B,C,D проведены параллельные прямые, пересекающие плоскость, сответственно в точках A1, B1, C1, D1. Найти длину отрезка DD1, если АА1=4м, ВВ1=3м и СС1=1м.
На ребре СС1 куба ABCDA1B1C1D1 отмечена точка Е так, что СЕ:ЕС1=1:2. Найдите угол между прямыми ВЕ и АС1
В прямоугольном параллелепипеде ABCDA1B1C1D1
BC=AA1=2, AB=3, точка M- середина BC.
Найти:
а) длину отрезка MD1
б)угол между A1M и AD1
в)расстояние от точки D до плоскости B1AM
г)угол между DM и плоскостью B1AM
д)угол между плоскостями B1AM и ACD1
12 й 4) В правильной шестиугольной призме ABCDEFA,B,C,D,E,F, Bce pebpa paBus! 2. Haiitn расстояние от точки С до прямой Ё, Е.

Осевым сечением конуса является равносторонний треугольник. Радиус основания 8 см. Найти высоту цилиндра
Правильная шестиугольная призма ABCDEFA1B1С1В1D1E1F1 все ребра которой равны 1, расположена в системе координат Oxyz так, что центр ее основания совпадает с началом координат, а вершины A, F, F1, В1 имеют координаты: A(√3/2; –1/2; 0), F(0; –1; 0), F1(0;–1;1), B1(√3/2; 1/2; 1).
Постройте эту призму и координатным методом найдите:
а) величину угла между прямыми АВ1 и СF1;
б) синус угла между прямой В1E и плоскостью ВС1С;
в) косинус угла между (АВС) и (ВС1F).
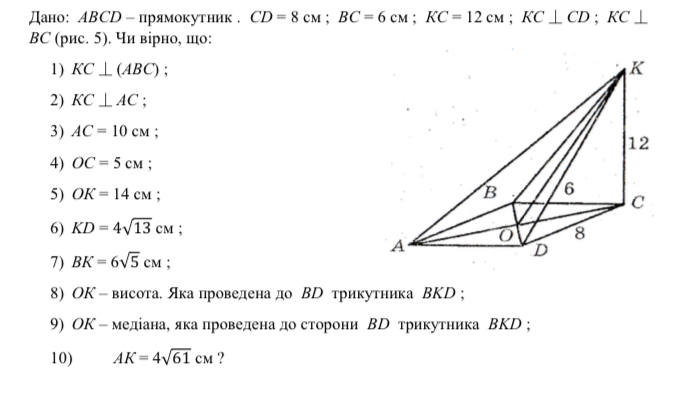
Дано: ABCD - прямокутник. CD = 8 см ; BC = 6 см ; KC = 12 см ; KC ⊥ CD ; KC ⊥ BC (рис. 5). Чи вірно, що:
1) KC ⊥ (ABC) ;
2) KC ⊥ AC ;
3) AC = 10 см ;
4) OC = 5 см ;
5) OK = 14 см ;
6) KD = 4 √13 см ;
7) BK = 6√5 см ;
8) OK - висота. Яка проведена до BD трикутника BKD ;
9) OK - медіана, яка проведена до сторони BD трикутника BKD ;
10) AK = 4√61 см ?
В правильной четырёхугольной призме ABCDA₁B₁C₁D₁ сторона основания равна 2, а боковое ребро равно 1. Найди угол между прямыми AA₁ и BD₁.
В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ даны длины рёбер:
AB=6, BC=4, AA₁=3. Найди угол между прямыми AC₁ и B₁C.
Решить8. Через вершину В р!внобедреного трикутника АВС (АВ = ВС) до площини трикутника проведено перпендикуляр ВК довжиною 5 ем. Знайти в!дстань в1д точки К ь;;…‚_-„‹›‚і‚*“ 5 › = & см, АВ = 6 м. ! ) il = ЕР

Найдите расстояние между диагональю A₁C₁ куба ABCDA₁B₁C₁D₁ c ребром 8 и прямой, проходящей через середины ребер BC и B₁C₁.
2) Дано: треугольник АВС, DS ⊥ (АВС), AD = VD
Построить линейный угол двугранного угла DAVS. Доказать, что именно он будет двугранным.
3) Дано: AVSD квадрат, VB ⊥ (AVC). Точку М соединили с вершинами квадрата.
Построить линейный угол двугранного угла MAVD. И доказать, что именно он будет двугранным.

1. Дано: MB ⊥ (ABC), MB = 3
MA = MC = 5,
AK = KC, ∠BCA = 30°
Найти расстояние от точки M до AC.
В кубе A...D1 найдите угол между прямой A1Bи плоскостью BCC1
Из точки лежащей вне плоскости проведены к этой плоскости две наклонные и перпендикуляр.Определите длину перпендикуляра, если наклонные равны 13см и 15 см, а разность их проекции равна 4 см
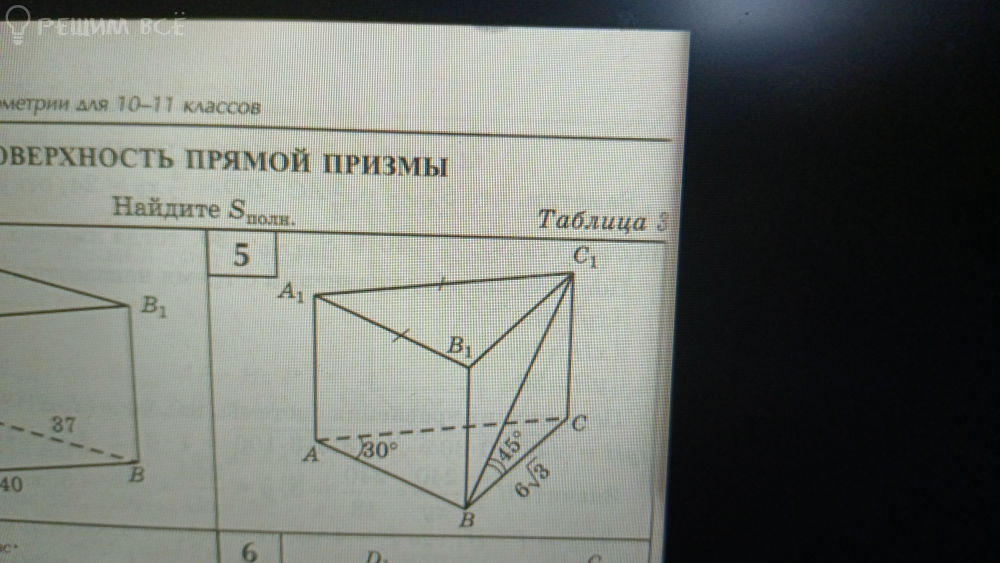
АВСА1В1С1 - правильная треугольная призма. d=13-диагональ боковой грани, h=6sqrt(3)-высота основания. Найдите а-сторону основания, b-боковое ребро, а- угол наклона диагонали боковой грани к плоскости основания, S осн.-площадь основания.
ABCDEFA1B1C1D1E1F1 правильная шестиугольная призма, все рёбра которой =1, найдите величину угла между прямыми Е1С и EF
Дан куб с ребром, равным 1. Найдите синус угла между прямой В1D u (ABC1).
Дан куб с ребром, равным 1. Найдите синус угла между (АВ1С) и (А1ВС).

Шар пересечен плоскостью на расстоянии 8 от его центра. Найдите радиус сечения, если радиус шара равен 15
В правельной треугольной призме abca1b1c1 все ребра которой равны 1 найти угол между прямыми ac и b1c1
Помогите пожалуйста!!!В правильной треугольной пирамиде боковое ребро образует с плоскостью основания угол 30 ° Найдите высоту пирамиды, если радиус описанной вокруг ее сферы равен 4
Задача 1. Жуку надо доползти по поверхности прямоугольного параллелепипеда из одной вершины в другую кратчайшим путем. Найти длину этого пути по указанным размерам.
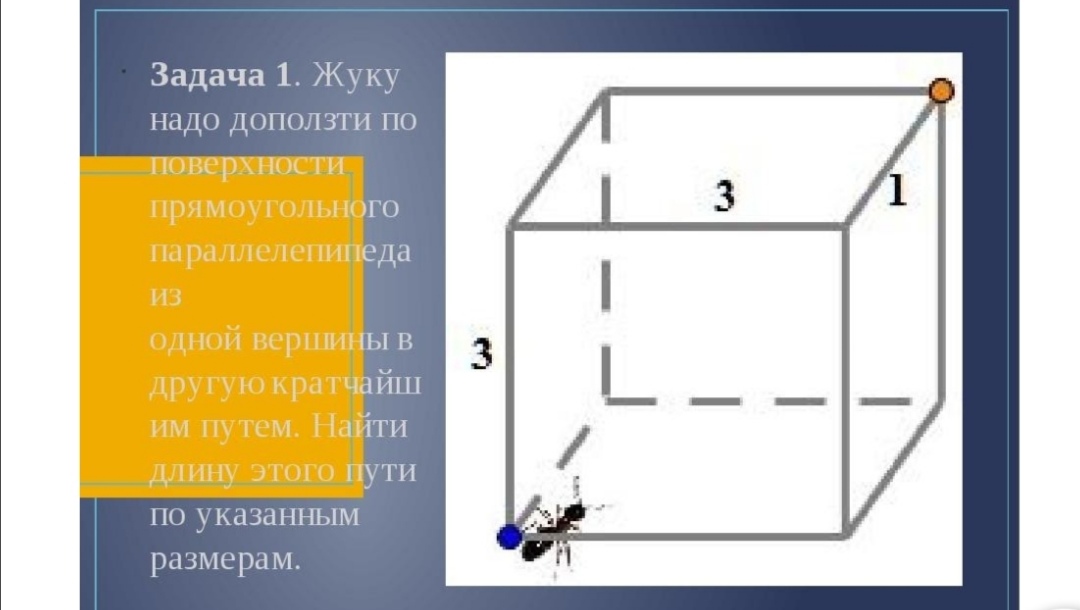
Таблица 10.11. Перпендикуляр и наклонная.
AA₁ - перпендикуляр к плоскости α, AB и AC - наклонные.
Найти x и y.
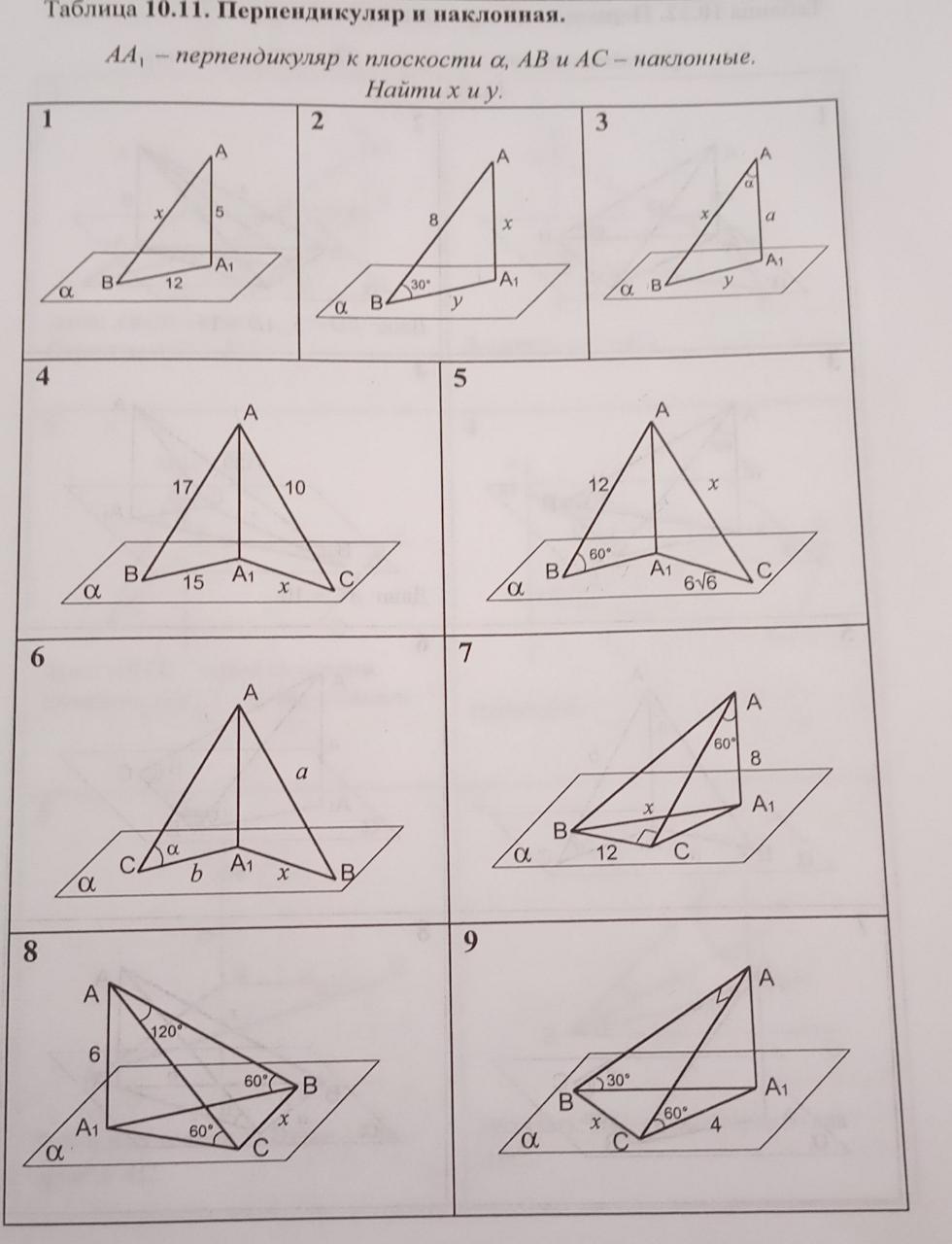
Условие представлено на картинке
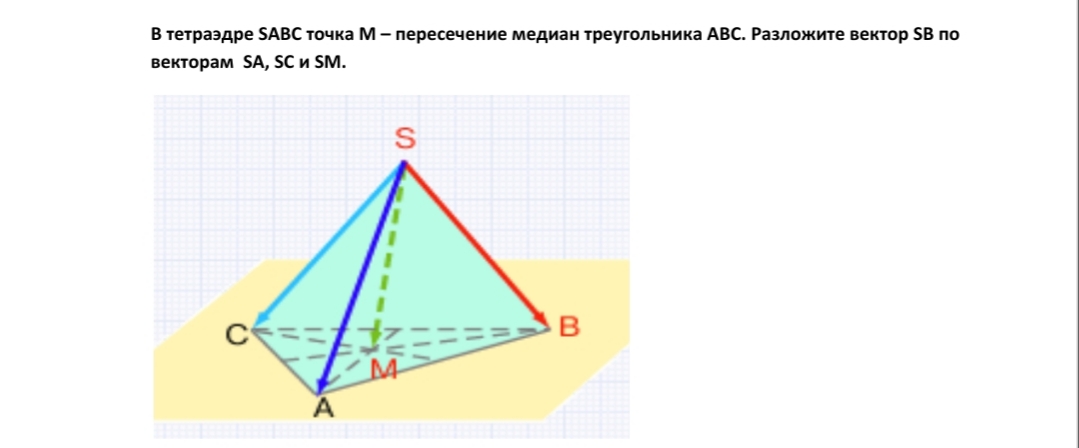
В основании пирамиды МАВСD лежит квадрат, а ее боковое ребро МС
перпендикулярно к плоскости основания и равно стороне основания. На ребрах
АВ, СD, МВ и МD взяты точки Р, Е, К и Т соответственно – середины этих ребер.
Найдите угол между КЕ и прямой:
а) ВТ; б) АD; в) СТ; г) ТР; д) МА; е) МD.
16.4. В правильной треугольной призме AVSAС, все ребра равны 1 (рис. 16.6). Найдите угол между: а) прямой АВС; б) прямой АВ и плоскостью ВСС!
Из вершины В квадрата АВСD проведен отрезок ВН, перпендикулярный плоскости квадрата, ВН = 10см. Прямая НА наклонена к плоскости квадрата под углом 45°. Найдите с точностью до 1° угол наклона прямой НD к плоскости квадрата
В кубе A...D1, найдите угол между прямой АB1 и плоскостью BCC1.
АВСД – прямоугольник. ВР перпендикулярно (АВС). Найдите РД, если АВ= 4, ВС = 6 и угол РСВ = 30°
плоскость y параллельная оси цилиндра отсекает от окружности основания дугу amd

Докажите, что прямая BD1 в кубе ABCDA1b1c1D1 перпендикулярна плоскости DA1C1.
правильной треугольной призме abca1b1c1 все ребра равны 1, найдите угол между прямыми ab1 и bc1
Дан прямоугольный параллелепипед ABCDABCD, в котором А A=4, а АВ=ВС=2. Вычислите косинус угла между векторами ВА1 и ВС1
Плоскость α пересекает стороны угла ВАС в точках А1 и В1, а параллельная ей плоскость β в точках А2 и В2. Найдите АА2 и АВ2, если А1А2=2, А1А=12, АВ1=5.
отрезок ак перпендикулярен к плоскости равнобедренного треугольника авс.известно что ав=ас=5см вс=4см ак=4см
выполните чертеж по условию задачи.
найдите расстояния от концов отрезка ак до прямой вс
В правильной треугольной призме ABCA1B1C1, все ребра которые равны единице , найдите угол между прямыми AC и BC1
В треугольнике ABC АВ = ВС = 10 см , АС = 12 см . через точку Вк плоскости треугольника проведен перпендикуляр BD длиной 15 см . а ) Выполните чертеж по условию задачи . b ) Найдите расстояние от концов отрезка BD до прямой АС .
Стороны основания правильной квадратной пирамиды SABCD равны 2 см, а высота – 1 см. Найдите расстояние от центра основания пирамиды О до плоскости SBC . Тема: Расстояние от точки до плоскости
Для прямоугольного параллелепипеда ABCDA1B1C1D1, у которого АВ=3, AD=4 , AA1=1, найдите косинус угла плоскостями АСD1 и АВС
Основание пирамиды представляет собой равнобедренный треугольник с длиной боковых сторон 5 см и углом между ними 120 °. Все боковые грани пирамиды образуют углы 45 ° с основанием пирамиды. Рассчитайте высоту пирамиды.
В основе пирамиды лежит равносторонний треугольник с основанием 6 см и высотой 9 см. Все стороны пирамиды равны 13 см. Вычислите высоту этой пирамиды.
площинами рівнобедрених трикутників ABC і ADC які мають спільну основу AC допівнюють 60 градусів знайдіть BD якщо AC = 24 см, кут ABC=60 градусів, кут ADC = 120 градусів

В правильной шестиугольной призме [m] ABCDEF A_1 B_1 C_1 D_1 E_1 F_1 [/m] на ребре [m] ЕЕ_1 [/m] отмечена точка [m] К [/m] так, что [m] ЕК : KE_1 = 2:1 [/m]. Найдите угол между плоскостями [m] A_1 B_1 C_1 [/m] и [m] ABK [/m], если [m] AB = 10 [/m] и [m] A A_1 = 6 \sqrt{3} [/m].
в правильной шестиугольной пирамиде S A B C D E F стороны основания 1 см боковые ребра 2 см найти угол между S C и (A B C)
Точка удалена от плоскости на 12см .Найти длину наклонной произведенной из этой точки под углом 45º к плоскости.
из точки лежащей вне плоскости проведены к этой плоскости две наклонные сумма длин которвх равна 12 дм. Проекции этих наклонных на плоскость 1дм и 7 дм.найти длину каждой наклонной и угол между плоскостью и большей наклоной
Найти угол между прямыми в правильной треугольной призме

Плоскость α пересекает стороны AB и AC треугольника ABC в точках B1 и C1 соответственно, BC || α . Найдите AC, если AC1 = 2см, BC:B1C1 = 2
SABCD - это правая прямоугольная пирамида. Стенки основания и высота 4 см. 1) BC 2) AC 3) Найдите синус угла между линией SC и плоскостью SAB.
чертеж
В основании прямой призмы лежит ромб с острым углом
60 ° и стороной 4 см Найдите диагонали призмы, если ее боковое ребро равно 6 см.
В пирамиде две равные боковые грани перпендикулярны основанию, а третья грань образует с основанием угол в 60 ° . Две равные стороны основания равны 15 м, а третья сторона 18 м.
а) Выполните чертёж.
б) Найдите высоту пирамиды.
в) Найдите длину боковых рёбер пирамиды.
a) Нарисуйте изображение правильной треугольной пирамиды. Изобразите апофему и высоту пирамиды.
b) Сторона основания правильной треугольной пирамиды равна 12 см, а боковое ребро – 2√19 см. а) Найдите высоту пирамиды. б) Найдите апофему пирамиды.
Помогите решить, пожалуйста!
Основой пирамиды есть прямоугольник со сторонами 18 см и 24 см. Каждый из боковых ребер равно 24 см. Найдите объем пирамиды.
Помогите с геометрией
Нужно подробное объяснение (для понимания)
Діагональ осьового перерізу циліндра дорівнює 8 см, з основою циліндра вона утворює кут 60 градусів. Знайдіть діаметр основи для цього циліндра
Решите 5, пожалуйста, методом координат

Решите 4, пожалуйста, методом координат

Решите 3, пожалуйста, методом координат

Решите 2, пожалуйста, методом координат

Основою піраміди є ромб, сторона якого дорівнює 12 см і гострий кут дорівнює 30 градусів. Усі двогранні кути при основі дорівнюють 60 градусів. Обчисли высоту і площу бічної поверхні піраміди
В основании четырехугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами АВ = 4 и ВС = 3. Длины боковых ребер пирамиды SA = sqrt(11) , SB = 3sqrt(3), SD = 2sqrt(5).
а) Докажите, что SA - высота пирамиды.
б) Найдите угол между прямой SС и плоскостью ASB.
В правильной треугольной призме ребра которой равны 1, найдите площадь сечения, проходящее через вершины ...
В правильной четырехугольной пирамиде SABCD все ребра равны 1, точка Е — середина ребра SC. Найдите угол между прямыми AD и BE
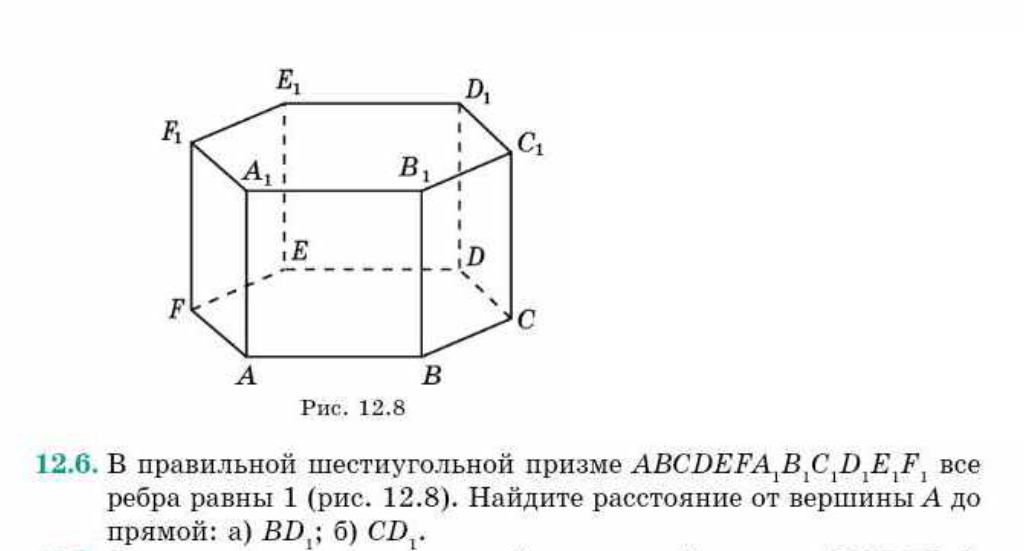
В правильной шестиугольной призме все ребра равны 1 (рис. 12.8). Найдите расстояние от вершины А до
прямой: а) ВD1 6) СD1
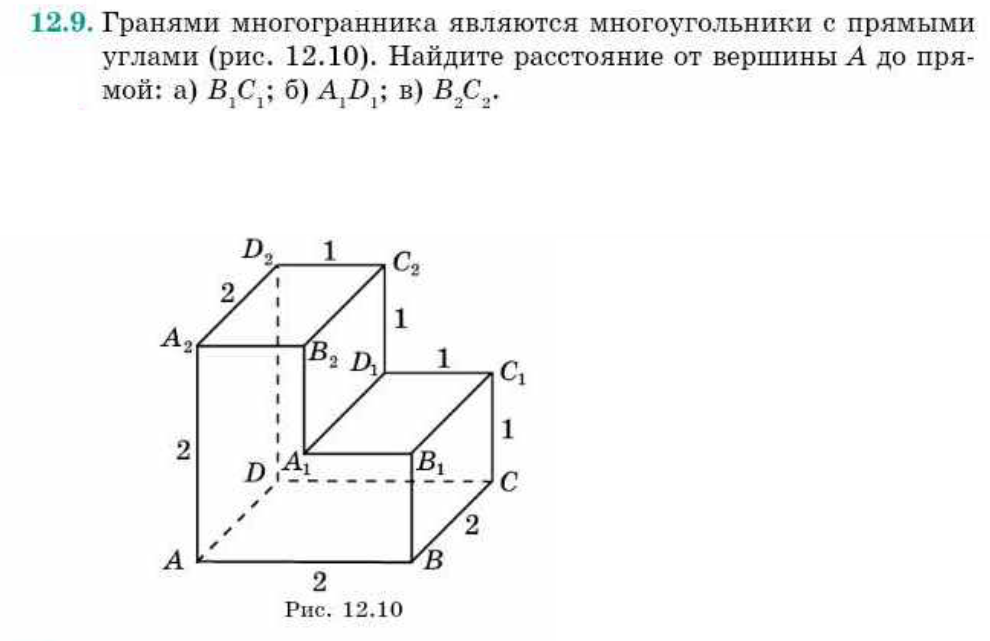
Гранями многогранника являются многоугольники с прямыми углами (рис. 12.10). Найдите расстояние между вершинами: ....

Гранями многогранника являются многоугольники с прямыми углами (рис. 12.10). Найдите расстояние от вершины А до пря-
мой: ...
Дан тетраэдр ABCD. Известно что AB=BC=CD=5 и CA=AD=DB=6. Найдите косинус угла между рёбрами BC и AD
Радиус основания цилиндра равен 13см,высота-24см. На каком расстоянии от оси цилиндра следует провести сечение,параллельное оси цилиндра,чтобы оно имело форму квадрата?
Выполнить рисунок правильной шестиугольной пирамиды.построить сечение пирамиды плоскостью паралельной основанию если данная плоскость делит высоту пирамиды в отношении 3:2 считая от высоты пирамиды.вычислитьплощадь полученного сечения если площадь основания пирамиды 50 см^(2),а высота пирамиды 15 см
В прямой треугольной призме стороны основания равны 11см 14см и 19см,а высота 7sqrt(3).вычислить площадь сечения проведенного через боковое ребро и большую высоту основания призмы
С чертежем пожалуйста
Відстань від точки S до сторони квадрата АВСD дорівнює 4√5 см, а радіус кола, вписаного в цей квадрат, дорівнює 8 см. Знайдвть відстань від точки S до площини квадрата.



















































