Задача 68633 геометрия 10 класс 8 задача!!:( с...
Условие
математика 10-11 класс
280
Решение
★
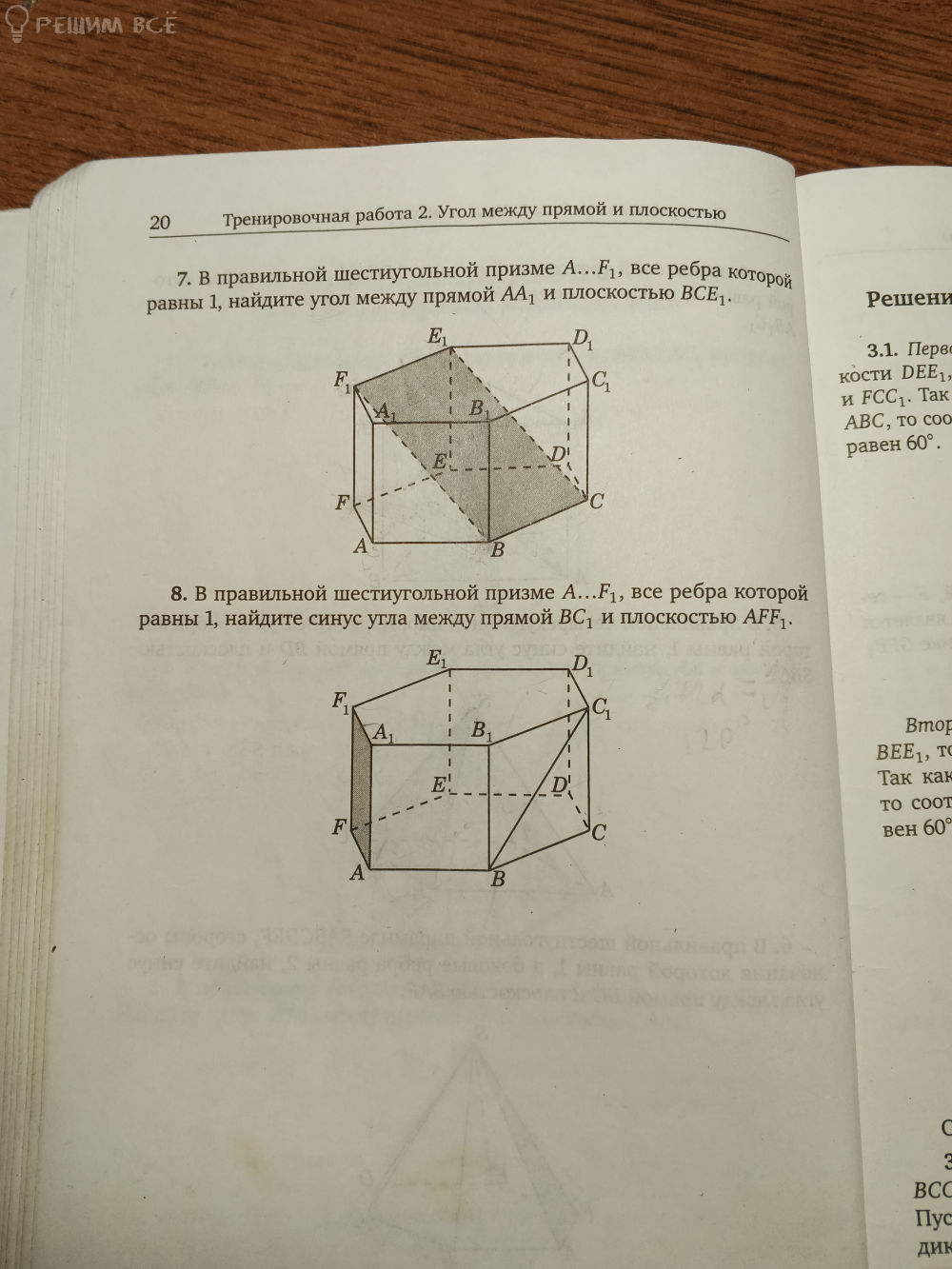
Обозначим
плоскость A_(1)A_(1)F_(1)F= α
A_(1)C_(1) ⊥ F_(1)A_(1)
A_(1)C_(1) ⊥ AA_(1) ⇒
Прямая A_(1)C_(1) перпендикулярна двум пересекающимся прямым плоскости ⇒
Прямая A_(1)C_(1) перпендикулярна плоскости α
Проводим BK || A_(1)C_(1)|| AC
⇒
BK ⊥ плоскости α
A_(1)K- проекция BC_(1)
Угол между прямой BC_(1) и прямой A_(1)K
найдем из прямоугольной трапеции A_(1)C_(1)BK ( см. рис)
KM || BC_(1)
По теореме Пифогра
KM^2=(3/2)^2+(sqrt(3)/2)^2=(9/4)+(3/4)=12/4=3
sin ∠ A_(1KM=A_(1)M/KM=sqrt(3)/(2*3)=[b]sqrt(3)/6[/b]
