Задача 76523 ...

66050714975c145645ee0812

3/28/2024 5:59:27 AM

Точка М находится на расстоянии 10 см от вершин равнобедренного треугольника АВС (АВ=ВС) и на расстоянии 6 см от его плоскости. Найти стороны треугольника, если ∠ВАС = 30
С дано и рисунком

5f3ea7e3faf909182968ddd9

3/28/2024 7:09:58 AM

★

MA=MB=MC=[b]10[/b]
Равные наклонные имеют равные проекции

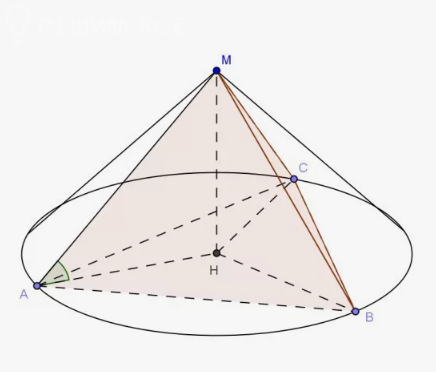
Н- проекция точки М на плоскость АВС

МН=[b]6[/b]

AН=BР=CН ⇒ Н - центр описанной около треугольника АВС окружности

АН^2=AM^2-MH^2=10^2-6^2=100-36=64

AH=8

Задача

В равнобедренном треугольнике (AB=BC)
радиус описанной окружности равен 8,
∠ВАС = 30 ° - вписанный угол


∠ВHС = 60 °- центральный угол, опирающийся на ту же дугу

Δ BHC- равнобедренный ( ВН=СН=8) и ∠ВHС = 60 ° ⇒ Δ BHC- [b]равносторонний[/b]

[b]ВС=8[/b]

[b]АВ=ВС=8[/b]

Дан равнобедренный треугольник АВС (AB=BC)

∠ВАС =∠ВСА=30 °

∠ АВС=180 ° -∠ВАС -∠ВСА =120 °

По теореме косинусов

AС^2=AB^2+BC^2-2*AB*BC*cos∠ АВС=8^2+8^2-2*8*8*(-1/2)=3*8^2
[b]
AC=8sqrt(3)[/b]