Задача 70933 ...

63fcc4398591dd4e26a53285

21.04.2023 17:03:30

З вершини прямого кута C трикутника ABC проведено перпендикуляр
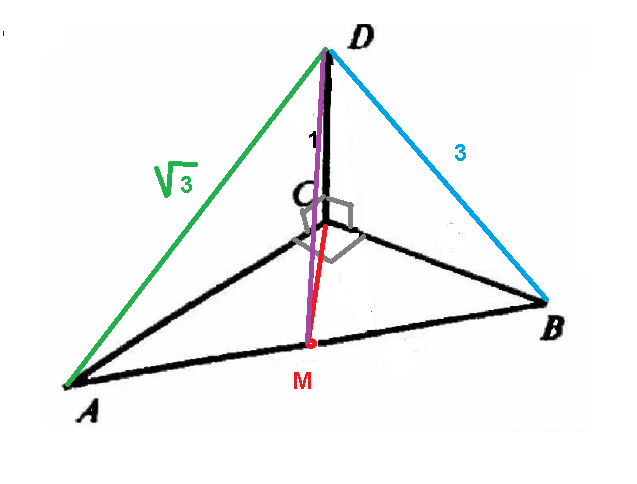
CD до площини трикутника. DB і DA - похилі.
Відомо, що:
CD = 1см;DB= 3см;DA=√3см
Знайти:
1. довжину невідомої похилої;
2. довжину невідомої проекції;
3. довжину відрізка АВ;
4. довжину медіани CM;
5. довжину відрізка DM;
6. відстань від точки В до площини DCM

5f3ea7e3faf909182968ddd9

21.04.2023 22:10:07

★

1. довжину невідомої похилої
их нет

2. довжину невідомої проекції;
СВ - проекция DB

CB^2=DB^2-CD^2=3^2-1^2=8
CB=sqrt(8)

CA - проекция DA

СA^2=DA^2-CD^2=(sqrt(3))^2-1=3-1=2
CA=sqrt(2)

3. довжину відрізка АВ;

АВ^2=AC^2+BC^2=8+2=10
AB=sqrt(10)

4. довжину медіани CM;

CM=(1/2)AB=sqrt(10)/2

5. довжину відрізка DM

DM^2=DC^2+CM^2=1^2+(sqrt(10)/2)^2=1+(10/4)=7/2
DM=sqrt(7)/2


6. відстань від точки В до площини DCM

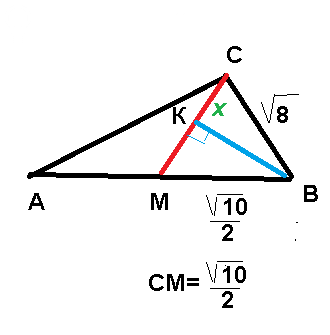
Расстояние равно длине перпендикуляра, проведенного из точки В на СМ

см рис. 2

Пусть СК=x

KM=(sqrt(10)/2)-x

ВК^2=BC^2-CK^2

BK^2=BM^2-KM^2


⇒ BC^2-CK^2=BM^2-KM^2

(sqrt(8))^2-x^2=(sqrt(10)/2)^2-((sqrt(10)/2)-x)^2

x=8/sqrt(10)

BK^2=8-(8/sqrt(10))^2=16/10

BK=4/sqrt(10)