Практика (11)
Задача 11. В правильной четырехугольной призме ABCDA1 B1C1D1 со стороной основания 4 и высотой 7 на ребре АА1 взята точка М так, что АМ=2. На ребре ВВ1 взята точка К так, что
В1К=2. Найдите угол между плоскостью, проходящей через точки D1, M, К и плоскостью СС1D1, расстояние от точки В1 до плоскости D1MK.
в правильной шестиугольной призме авсдеFа1 в1 с1 д1 е1 F1 известно что АВ=2 АА1=3 Найт расстояние от точки F до палоскости АДС1
1. В правильной треугольной призме ABCA1B1C1, где ВС - сторона основания, равна 12, а боковое ребро AA1 равно 3√6. На ребрах AB и B1C1 отмечены точки K и L соответственно, причем AK = 2, а B1L = 4. Точка М - середина ребра A1C1. Плоскость u параллельна ребру AC и содержит точки K и L.
a) Докажите, что прямая BM перпендикулярна плоскости u.
б) Найдите расстояние от точки С до плоскости u.
Даны четыре точки А1(4,2,10), А2(1,2,0), А3(3,5,7), А4(2,–3,5)
Вычислить:
а) синус угла между прямой А1А4 и плоскостью А1А2А3
б)косинус угла между координатной плоскостью Оху и плоскостью А1А2А3
а что дальше делать скажите:(
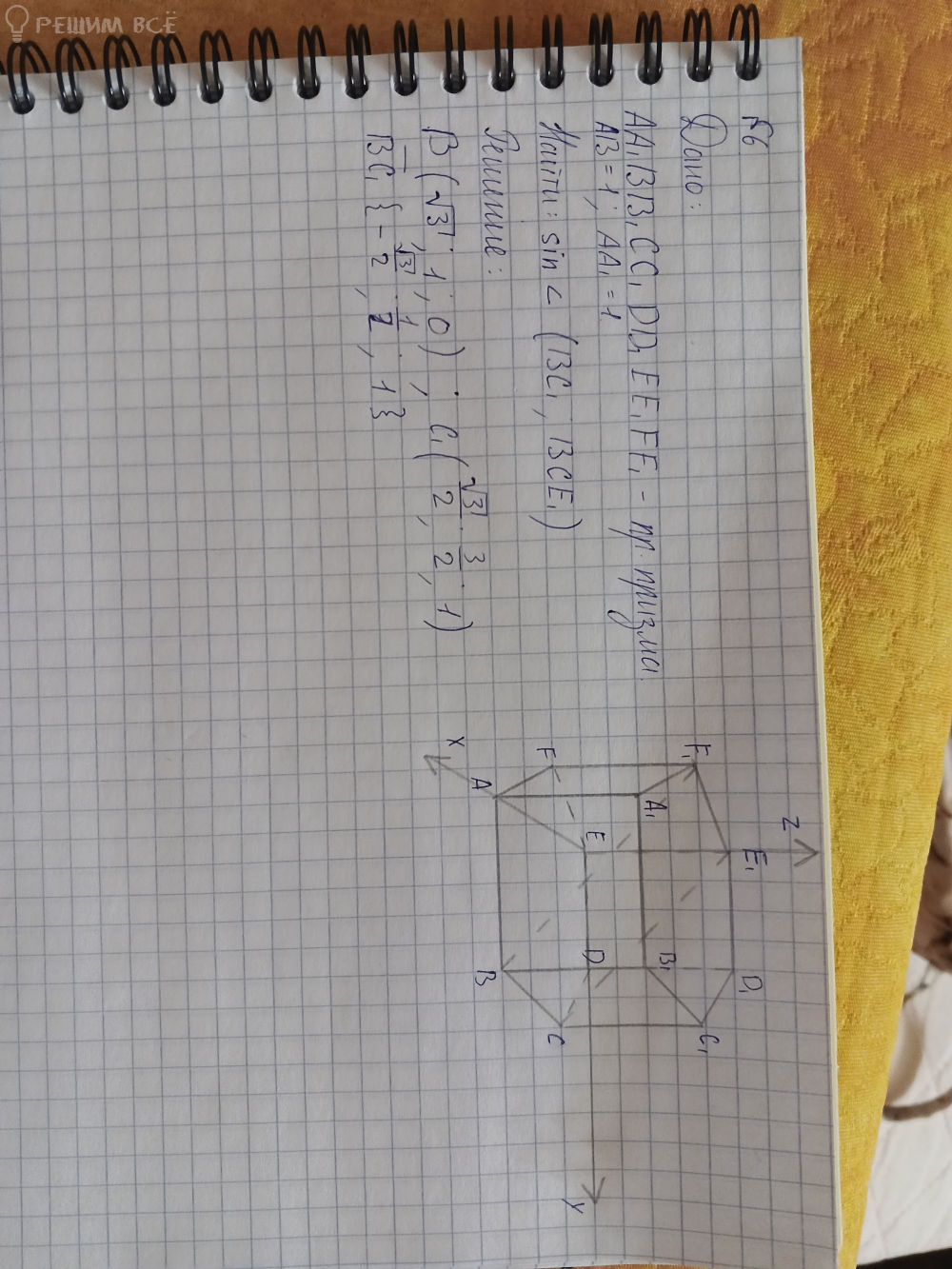
геометрия, координатные прямые 6 номер
ABCDA1B1C1D1 - прямой параллелепипед 3*3*6
AK:KA1=1:2
CT:TD=1:2
DM:MD1=2:1
BN:NB1=1:5
Найти: 1) (KT^MN)
2) (NM^AA1D1
3) (KT^CC1)
ABCD-тетраэдр, все боковые грани - прямоугольные треугольники. α - плоскость основания ABC
ABC: x/2+y/3+z/5=1
Найти: S основания и высоту тетраэдра.
Написать уравнения сторон равнобочной трапеции, зная, что основания ее соответственно равны 10 и 6, а боковые стороны образуют с основанием угол 60° . За ось Оx берется большее основание, за ось Oy – ось симметрии трапеции, а за положительное направление оси Oy – направление луча, пересекающего меньшее основание.
Задание 6. Найти угол между прямой А1В и плоскостью АСД1 координатно векторным способом
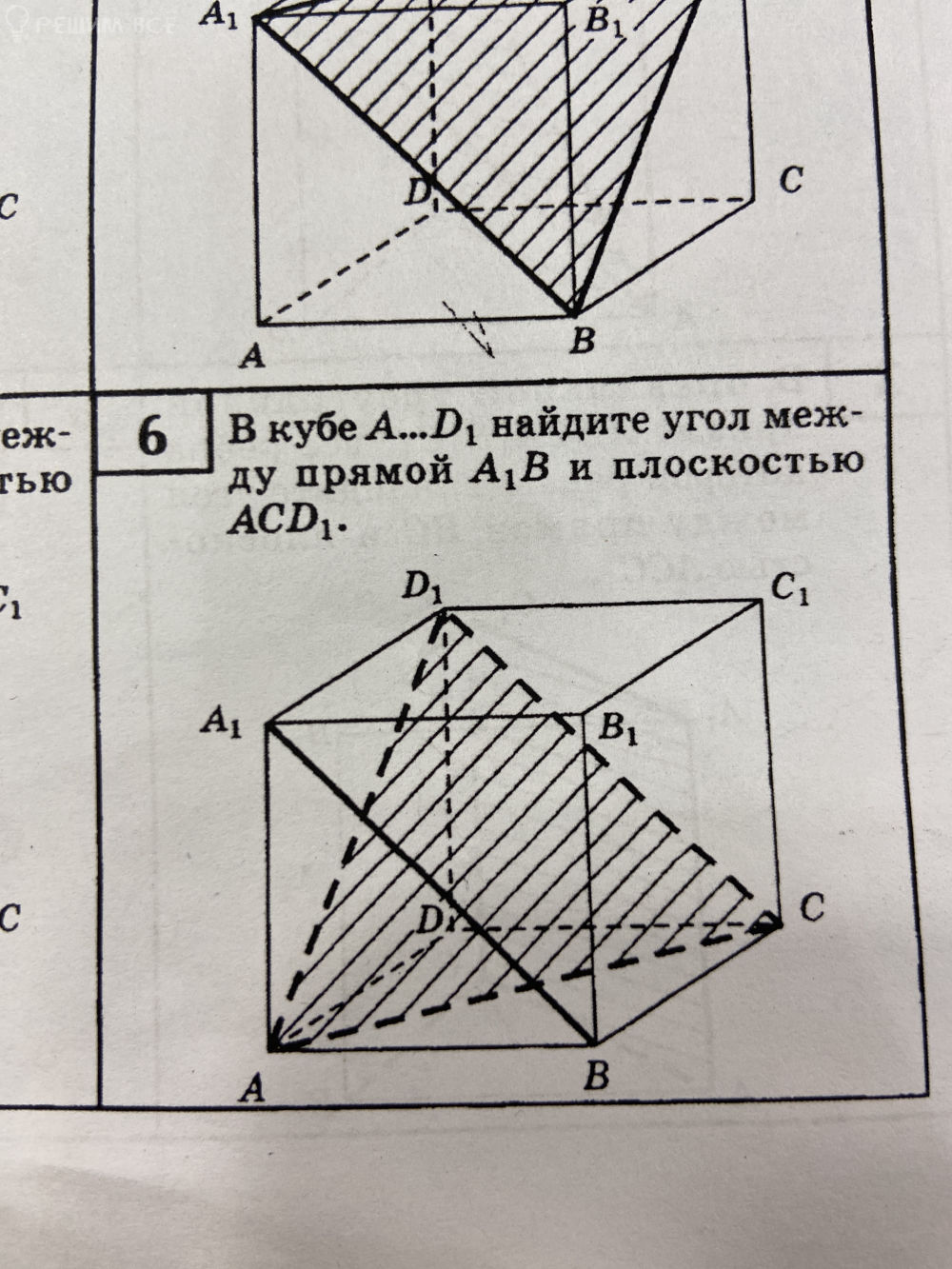
Буду рада хотя бы хорошему, понятному чертежу. А решению ещё больше).
при каком значении параметра а точки А(1, 3, 1), B(2,3,0), С(-1,2,1) и D (a+2, 4, 0) лежат в одной плоскости?