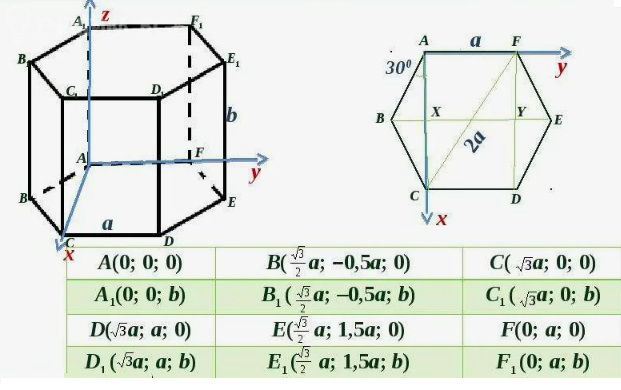
Задача 75980 в правильной шестиугольной призме...
Условие
Решение
См. скрин.
Уравнение плоскости АДС_(1) запишем в виде
ax+by+cz+d=0
Подставляем координаты точки А (0;0;0)
a*0+b*0+с*0+d=0 ⇒ d=0
Подставляем координаты точки D (2sqrt(3);2;0)
2sqrt(3)*a+2*b=0⇒ b=-sqrt(3)*a
Подставляем координаты точки C_(1) (2sqrt(3);0;3)
2sqrt(3)*a+0*b+3*c=0 ⇒c=-2sqrt(3)a/3
Подставим коэффициенты b; c в уравнение плоскости
a*x-sqrt(3)*a*y-(2sqrt(3)/3)*a*z=0
Делим на a
x-sqrt(3)*y-(2sqrt(3)/3)*z=0
F(0;2;0)
По формуле ( см . скрин)
[m] ρ (F, ADC_{1})=\frac{|0-2\sqrt{3}-0|}{\sqrt{1^2+(-\sqrt{3})^2+(\frac{2\sqrt{3}}{3})^2}}=\frac{3}{\sqrt{5}}[/m]