Задача 76053 ...

6518464ef2c01b1b41753cc6

2/29/2024 4:41:09 PM

1. В правильной треугольной призме ABCA1B1C1, где ВС - сторона основания, равна 12, а боковое ребро AA1 равно 3√6. На ребрах AB и B1C1 отмечены точки K и L соответственно, причем AK = 2, а B1L = 4. Точка М - середина ребра A1C1. Плоскость u параллельна ребру AC и содержит точки K и L.

a) Докажите, что прямая BM перпендикулярна плоскости u.

б) Найдите расстояние от точки С до плоскости u.

5f3ea7e3faf909182968ddd9

3/1/2024 1:57:36 PM

★

Геометрическое решение см на сайте
https://math-ege.sdamgia.ru/problem?id=514527

Решаем координатным методом.

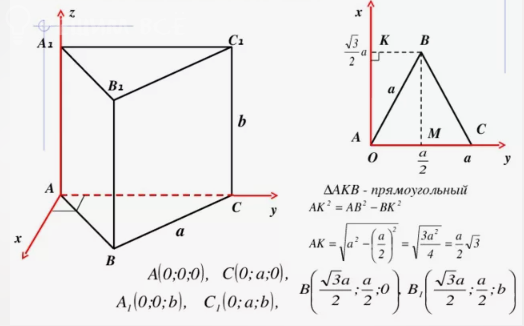
A(0;0;0)
C(0;12;0)
B(6sqrt(3);6;0)
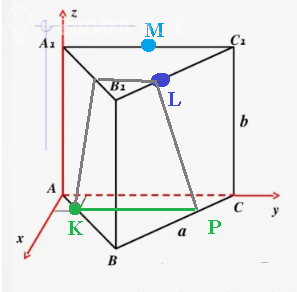
K(sqrt(3);1;0)
L(4sqrt(3);10;3sqrt(6))
M(0;6;3sqrt(6))

vector{BM}=(-6sqrt(3); 0;3sqrt(6))

vector{KP}=(0;10;0)

vector{LK}=(-3sqrt(3);9;-3sqrt(6))

Находим скалярное произведение векторов
vector{BM}*vector{KP}=0

vector{BM}*vector{LK}=0

⇒ Прямая BM перпендикулярна двум пересекающимся прямым плоскости, значит перпендикулярна всей плоскости.

Уравнение плоскости LKP запишем в виде:

ax+by+cz+d=0

Подставляем координаты точек

K(sqrt(3);1;0)
a*sqrt(3)+b+c*0+d=0

P(sqrt(3);11;0)
a*sqrt(3)+11b+c*0+d=0

Из этих двух равенств b=0

Тогда

asqrt(3)+d=0

d=-asqrt(3)



L(4sqrt(3);10;3sqrt(6))
a*4sqrt(3)+10*0+c*3sqrt(6)+d=0 ⇒
a*4sqrt(3)+c*3sqrt(6)-a*sqrt(3)=0

c=-a/sqrt(2)

получим уравнение


ax-(a/sqrt(2)z-asqrt(3)=0

сокращаем на а

x-(1/sqrt(2))z-sqrt(3)=0

[m]d=\frac{|-\sqrt{3}|}{\sqrt{1^2+(-\frac{1}{\sqrt{2}})^2}}[/m]

[m]d=\sqrt{2}[/m]