Задача 68771 а что дальше делать скажите:(...
Условие
геометрия, координатные прямые 6 номер 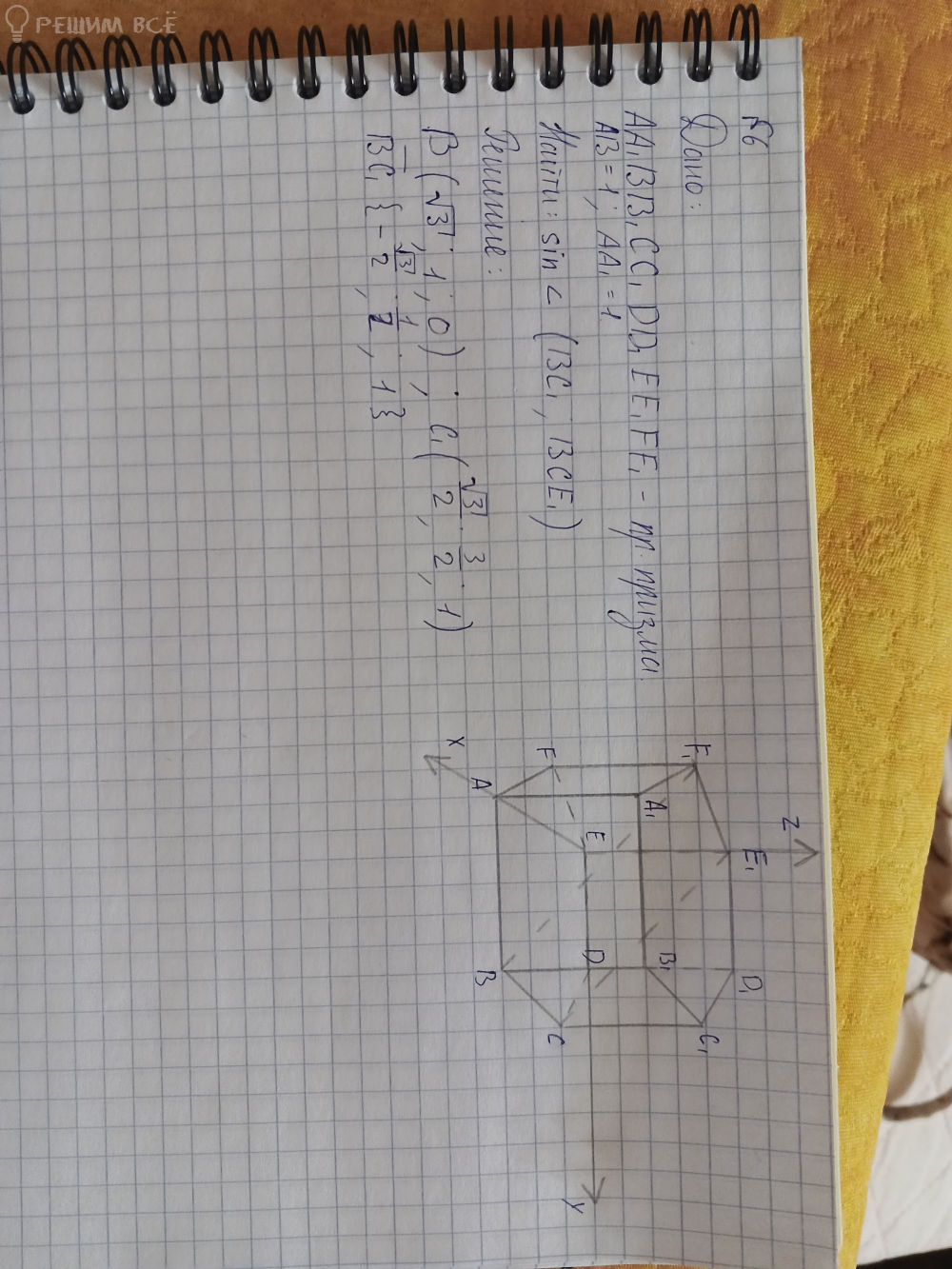
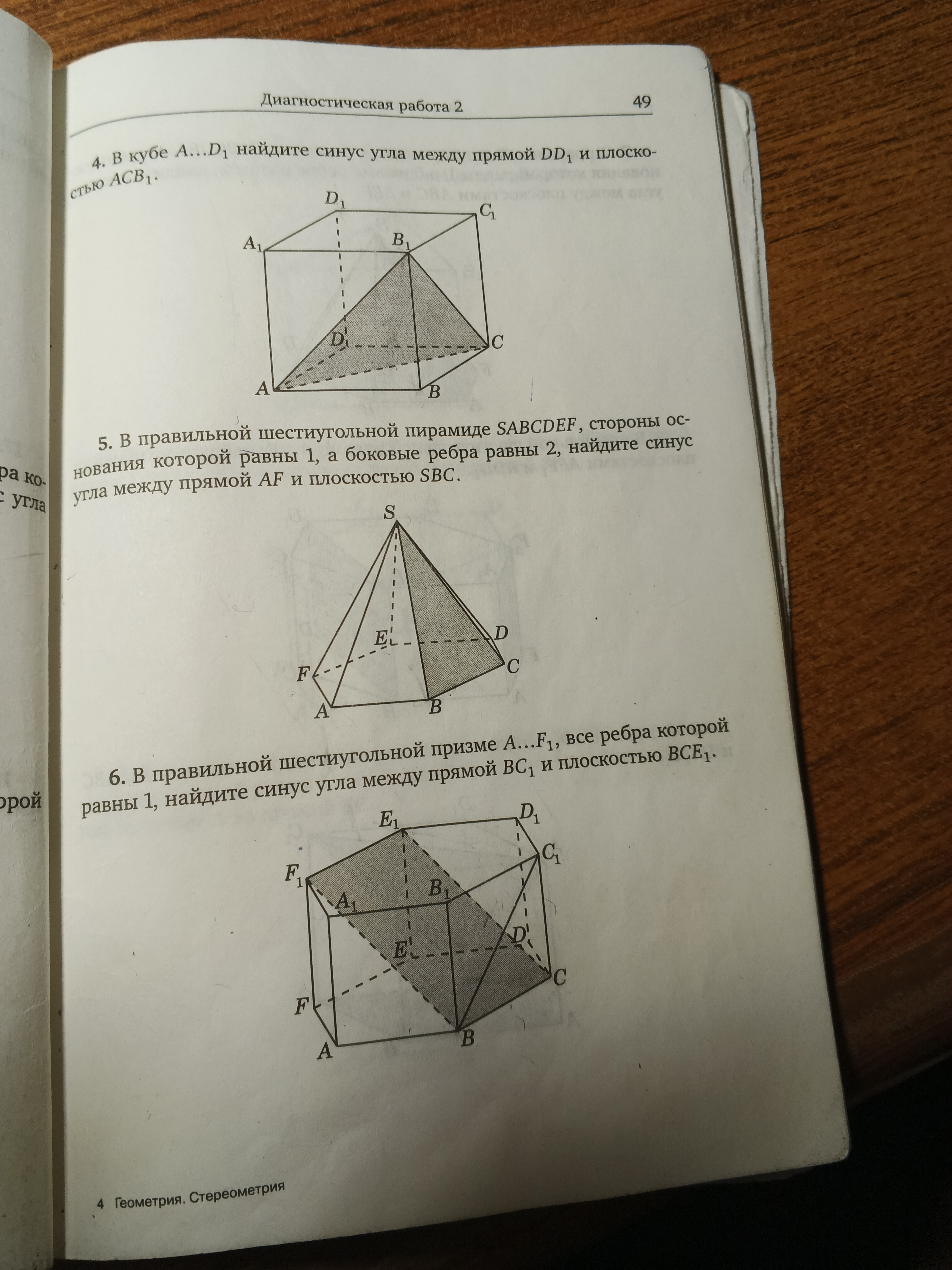
математика 10-11 класс
275
Решение
★
ВСЕ_(1)
ax+by+cz+d=0
Подставляем координаты точек
E_(1)(0;0;1)
a*0+b*0+c*1+d=0 ⇒ c=-d
B(sqrt(3);1;0)
a*sqrt(3)+b*1+c*0+d=0 ⇒ [b]d=-sqrt(3)*a-b[/b]
C(sqrt(3)/2; 3/2;0)
a*sqrt(3)/2+b*(3/2)+c*0+d=0 ⇒ [b]d=-(sqrt(3)/2)*a-(3/2)b[/b]
Приравниваем
[b]-sqrt(3)*a-b=-(sqrt(3)/2)*a-(3/2)b[/b] ⇒ b=sqrt(3)a
d=-sqrt(3)*a-b=-sqrt(3)*a-sqrt(3)a=-2sqrt(3)a
c=-d
c=2sqrt(3)a
Подставляем в уравнение
ax+by+cz+d=0
ax+sqrt(3)ay+2sqrt(3)az-2sqrt(3)a=0
Сокращаем на а
x+sqrt(3)y+2sqrt(3)z-2sqrt(3)=0 - уравнение плоскости ВСЕ_(1)
с нормальным вектором vector{n}=(1;sqrt(3);-2sqrt(3))
Угол между векторами: