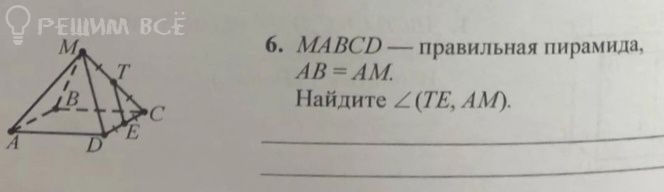Практика (77)
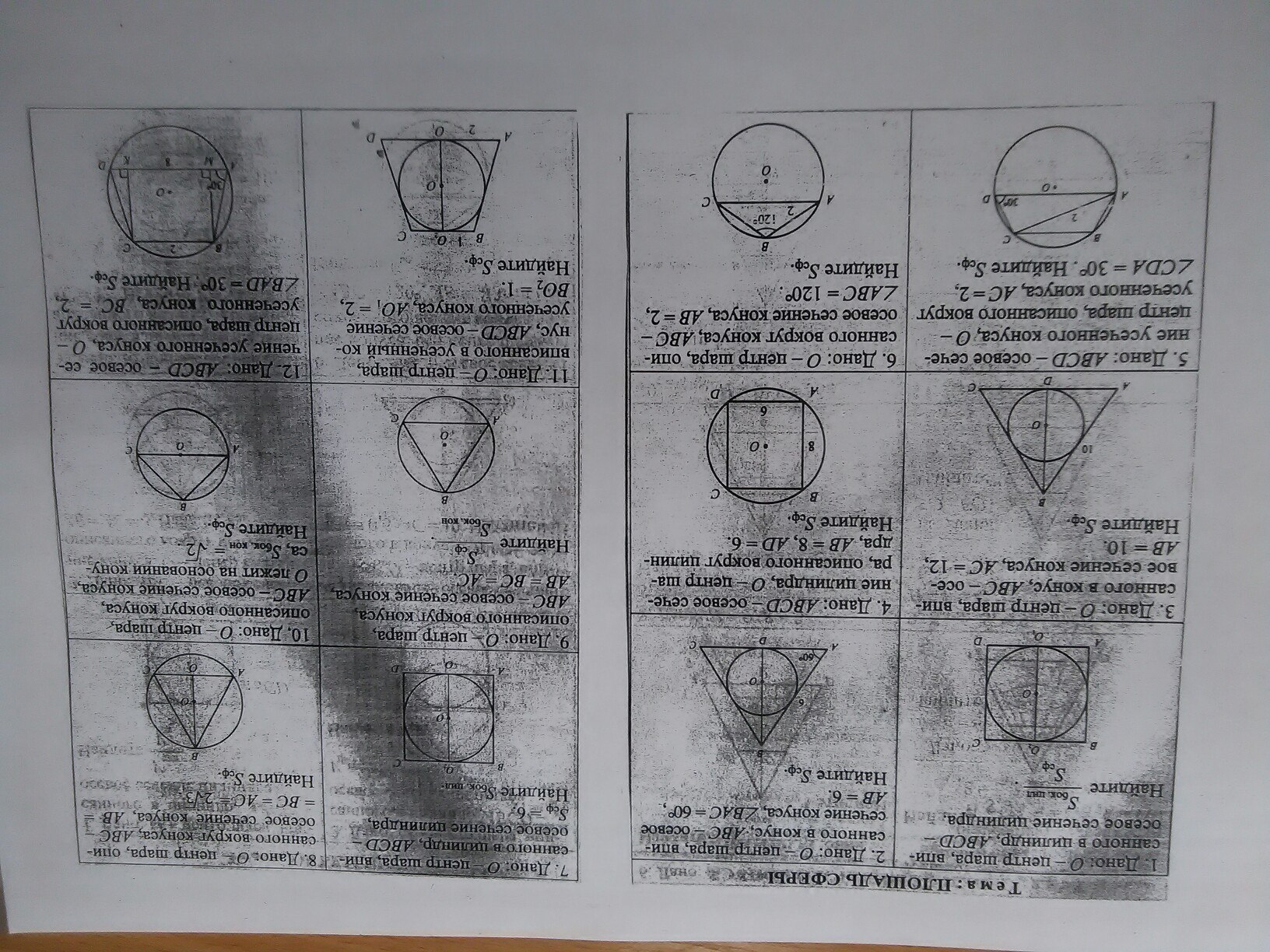
Найдите объем тела, полученного при вращении прямоугольного треугольника с катетами 6 см и 10 см вокруг меньшего катета.
В основании треугольной усеченной пирамиды ABCA1B1C1 лежит прямоугольный треугольник ABC. Ребро AA1 перпендикулярно плоскости основания. Вычисли указанные величины, если AA1 = 8, AC = 20, AC1 = 5 и AB = 21.

Боковая грань усечённой четырёхугольной пирамиды наклонена к плоскости основания под углом
60°. Найди площадь полной поверхности пирамиды, если высота пирамиды равна
5√3, а сторона меньшего основания 4
Ребро основания правильной треугольной пирамиды 3 м, апофема 6м.
Найдите площадь боковой поверхности пирамиды
Диагонали диагонального сечения прямоугольного параллелепипеда ABCD A_(1)B_(1)C_(1)D_(1) перпендикулярны. Вычисли объём, если AB=√2 см; BB_(1)=√11см.

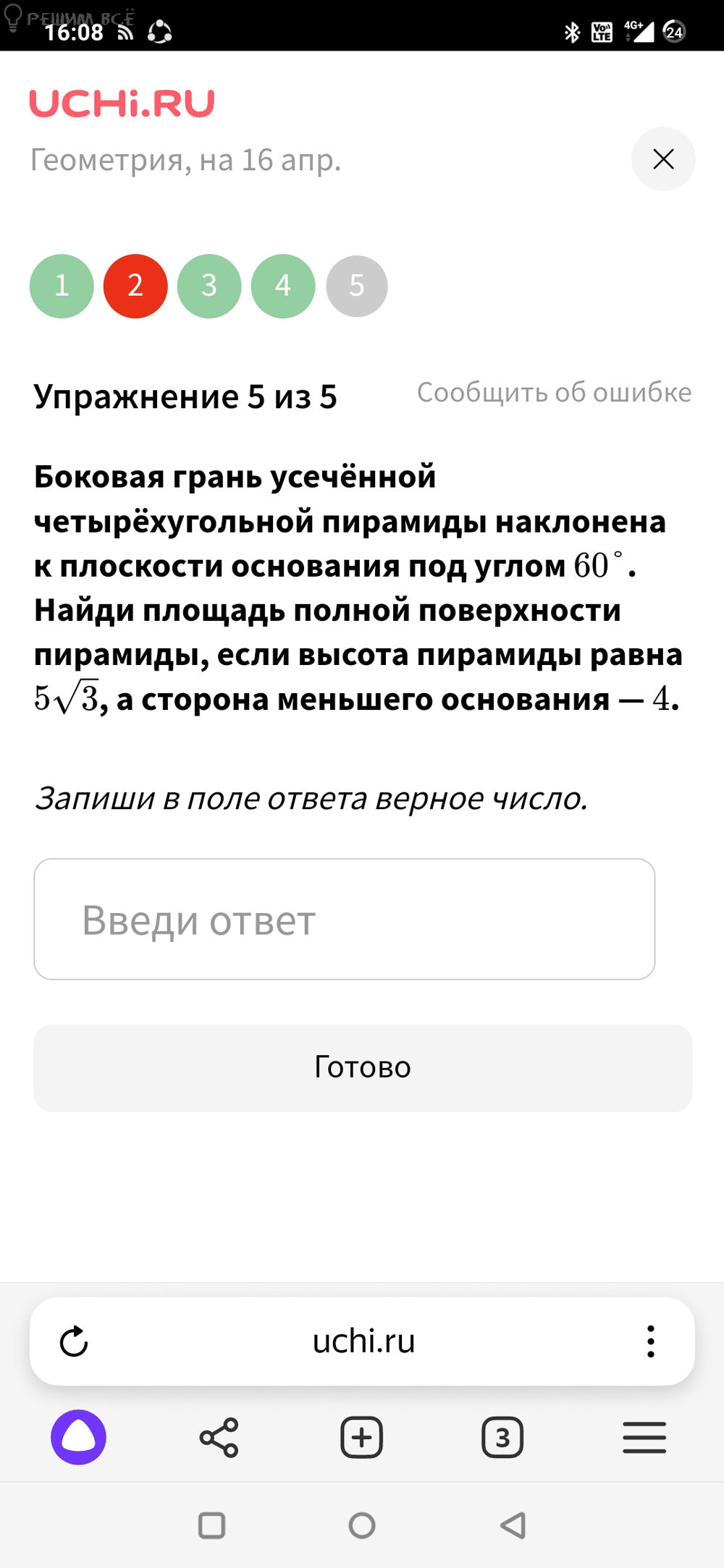
Площадь диагонального сечения куба равна 400√2 см^(2). Вычисли:
a) длину диагонали куба;
b) площадь поверхности куба;
c) объём куба.
ЗАДАЧА No3
У тетраедрі ОАВС з вершини О проведені медіани бічних граней.Беручи їх за ребра нового тетраедра, довести, що об’єм його становить 0,25 об’єму тетраедра ОАВС.
Через диагональ нижней и вершину верхнего основания правильной четырехугольной призмы проведена плоскость, которая пересекает две смежные боковые грани призмы по прямым, образующим между собой
угол 60°. Вычислите боковую поверхность призмы, если сторона основания равна а
В правильной четырёхугольной пирамиде высота образует с боковой гранью угол a. Отрезок, соединяющий основание высоты с серединой апофемы, равен с. Найдите полную поверхность пирамиды.
Задана правильная шестиугольная пирамида, высота которой равна 8. Угол между высотой и апофемой пирамиды равен 60°.
Определите длину стороны основания пирамиды (12 баллов).
Определите длину бокового ребра пирамиды (10 баллов).
Вычислите объём пирамиды (10 баллов).
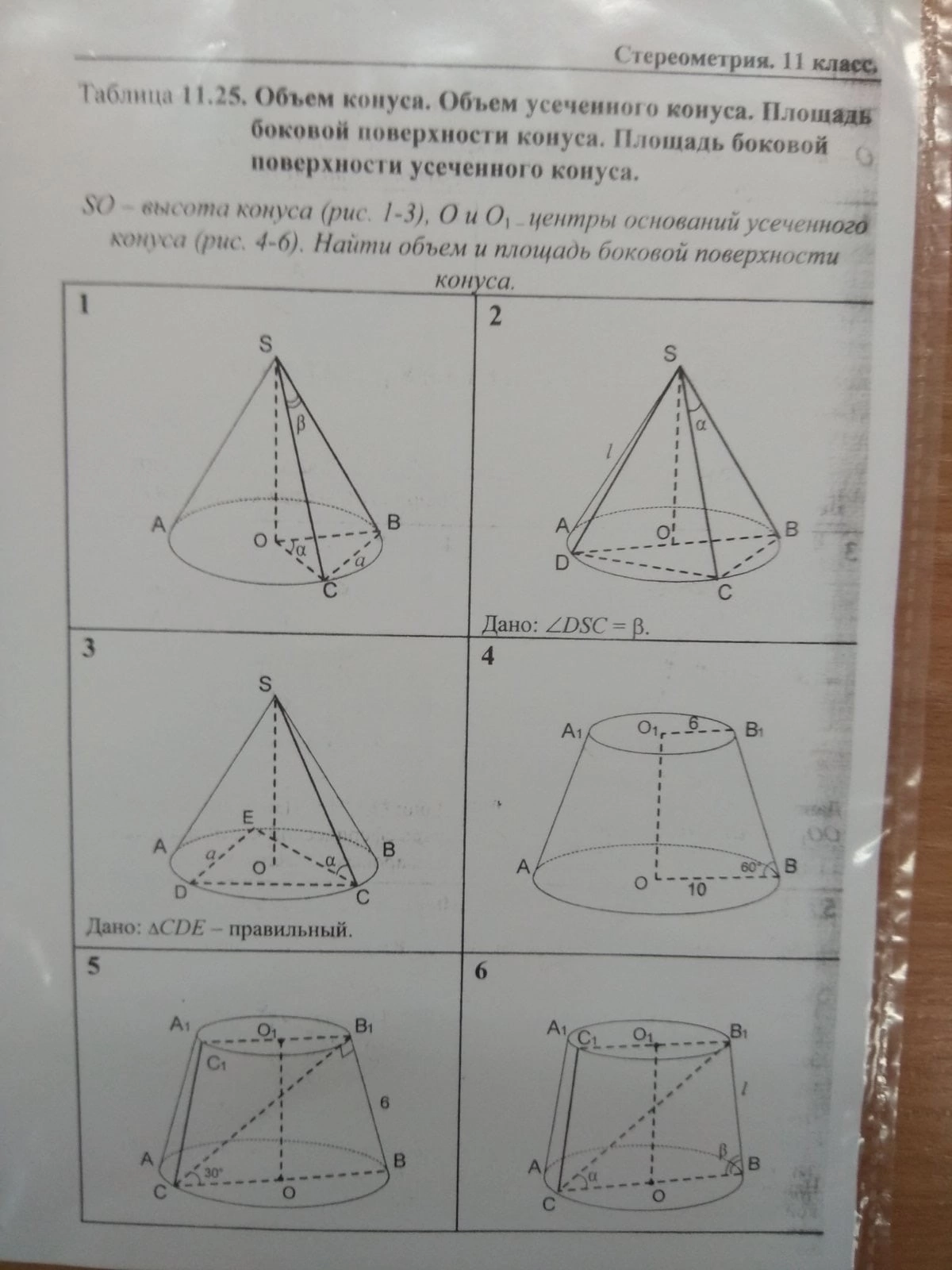
Таблица 11,25, Объем конуся, Объем усеченного конуса. Площадв боковой поверхности конуса. Площадь боковой y поверхности усеченного конуса. О - высота конуса (рис. 1-3), O u О, - центры оснований усеченног конуса (рис. 4-6). Найти объем и площадь боковой поверхности
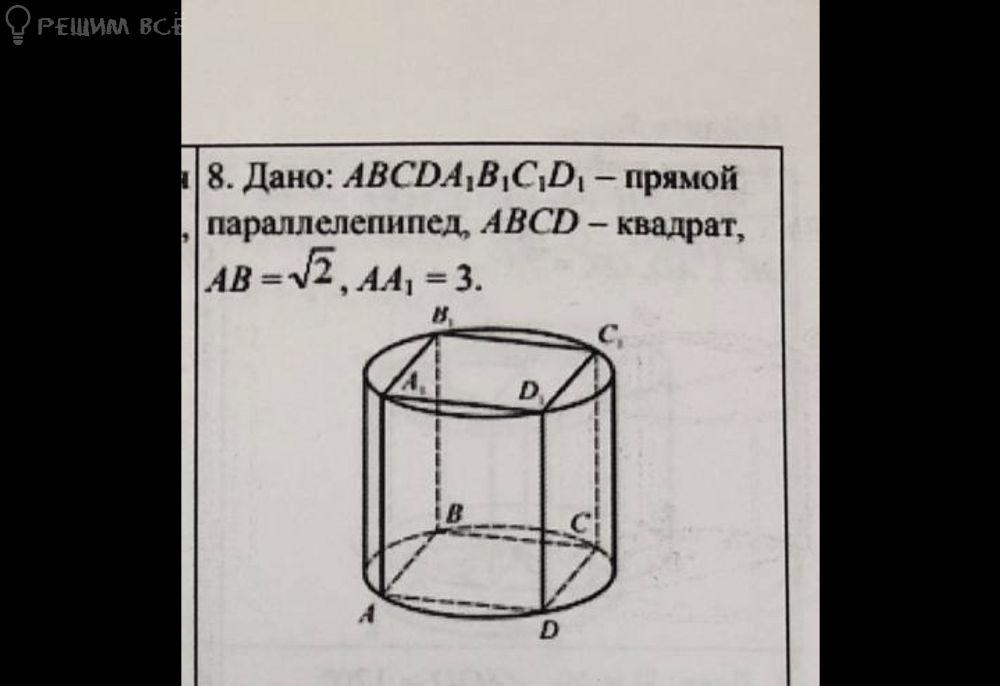
Дано: ABCDA1B1C1D - прямой параллелепипед, ABCD - квадрат,
AB =12, AA = 3. Найти площадь бок. Цилиндра -?
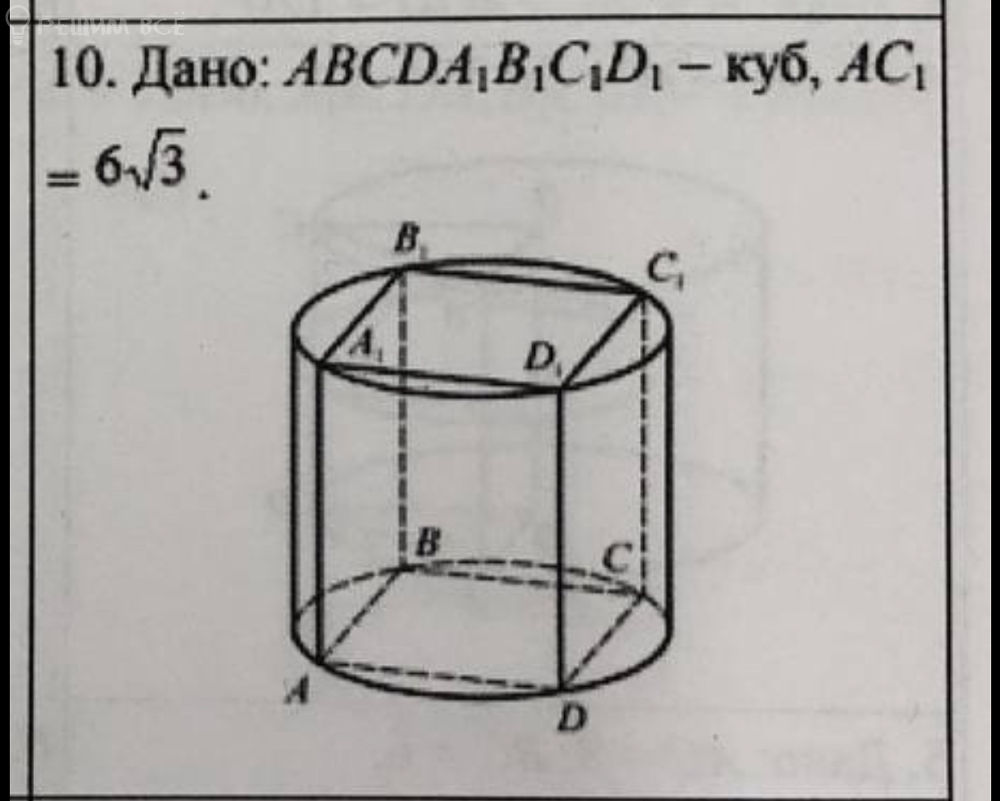
Дано: ABCDA1B1C1D1 - куб, AC1 = 6/корень из 3. Найти площадь бок.цилиндра-?
Стороны основания прямоугольного параллелепипеда относится как 2:14 , длины диагонали боковых граней равны 26 см и 74 . найти площадь полной поверхности
6. Основа прямої призми - ромб з діагоналями 4 см і 4√3 см. Обчислити площу повної поверхні
присми, якщо її більша діагональ утворює з основою кут 60 °.

Основою піраміди є ромб, сторона якого дорівнює 40 см і гострий кут дорівнює 30°.
Усі кути, які утворюють бічні грані з площиною основи, дорівнюють60°.
Обчисли висоту і площу бічної поверхні піраміди.
Висота піраміди дорівнює
Площа бічної поверхні дорівнює
В цилиндре радиус основания и высота цилиндра соответственно равны 4см и 15 см . Найти:
1) диаметр основания;
2) диагональ осевого сечения:
3) угол наклона диагонали осевого сечения к плоскости основания;
4) площадь основания цилиндра;
5) площадь осевого сечения;
6) длину окружности основания.
Диагональ основания правильной шестиугольной пирамиды равна 24 см, а боковое
ребро пирамиды – 13 см. Сторона основания равна 4 см. Найдите объем пирамиды.
Дана правильная треугольная призма. Сторона основание–12см, высота –9см. Найти её полную поверхность и объем.
Спасибо за раннее!)
Діагональ правильної чотирикутної призми дорівнює d i нахилена до площини основи під кутом ф. Знайдіть площу: а) діагонального перерізу; 2) бічної поверхні призми.
Решите
e v o ‚@‚ 8 © ГОО = 73 .' НОа ое BEgREF if{;s В ® Ё B NT _“-. © Ё %5 2 E o . i--. Ё Е “ $ B Egsdgs DT AEELE О: ЗЕ ЗЕНЕ И ВЫ с в ВЕО EHEE | 1 ВЕ 273 e R =32 ЕН Y | S g НО ВОН ВЕЁ | 4 2258 B в НН , B й88 L fi,fllllllllll Е& Зей S Е %'Ё Е —- @Ё"-"'---' 338:d аННЕ ВВееОНННННН +TLL i sfiu-l----lnl P B :gfifllllllllllll! а° … ‚_„_.__‚_._‚‚:.‚›….аи-ппппп 38 ‚…;.‚—.„шн----ппп EEECY .mln--l---lll » ч_нп--ппппп 8 е „*з_:----п-ппп вавЕ ®) ‚:.-‚__…я------пч В а8 82 ©2 ” ‚.'ЯП'--"-'--"" 588g & < Е НО& НЕ 88 (

в прямом параллелепипеде проведено сечение через диагональ нижнего основания и середину непересекающегося с этой диагональю бокового ребра. Объем меньшего из двух многогранников на которые параллелепипед делится плоскостью сечения, равен 40см^3 Найдите объем параллелепипеда
Высота конуса 6 см, образующая – 10 см. Найти площадь осевого сечения, площадь боковой поверхности конуса, площадь полной поверхности конуса.
Основою піраміди є прямокутний трикутник з катетами 5 см і 12 см. Усі двогранні кути при основі рівні 60°.
Обчисли висоту бічної грані піраміди.
В цилиндре
параллельно его оси
проведена плоскость,
пересекающая нижнее
основание цилиндра по
хорде, которую видно
из центра этого
основания под углом α.
Найдите площадь
боковой поверхности
цилиндра, если площадь
образовавшегося
сечения равна S.
Сечением наклонного параллелепипеда ????????????????????1????1????1????1,
перпендикулярным к боковому ребру, является ромб ???????????????? со
стороной 6 см и углом 60°, большая диагональ которого равна
боковому ребру параллелепипеда. Найдите объем
параллелепипеда.
Пирамида, в основании которой лежит ромб с острым
углом ????, описана около конуса радиуса ????. Образующая конуса
составляет с плоскостью основания угол ????. Найдите объем
пирамиды
Пирамида, в основании которой лежит ромб с острым
углом ????, описана около конуса радиуса ????. Образующая конуса
составляет с плоскостью основания угол ????. Найдите объем пирамиды.
B основании пирамиды МABCD параллелограмм ABCD. В каком отношении, считая от вершины, делит объем пирамиды сечение, проходящее через ребро АВ и середину реб pa MC?
Площадь основания конуса равна 25 π, высота - 4. Найти площадь осевого сечения конуса
Объем и высота цилиндра равны соответственно 128п и 2, а другого - 24п и 6. Во сколько раз радиус основания первого цилиндра больше радиуса основания второго цилиндра
Сечение конуса плоскостью, параллельной основанию, делит высоту на отрезки 2 и 6 начиная от вершины конуса. Найди объём конуса, если площадь сечения равна 56
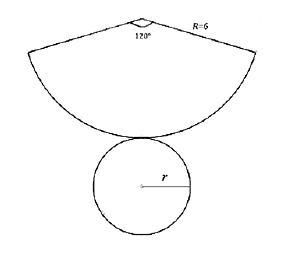
Радиус кругового сектора равен 6 см, а его угол равен 120 градусов. Сектор свернут в коническую поверхность.
Найдите:
a) площадь бедренную стороны конуса
b) покажите основания радиуса конуса r=2
с) площадь полной поверхности конуса.
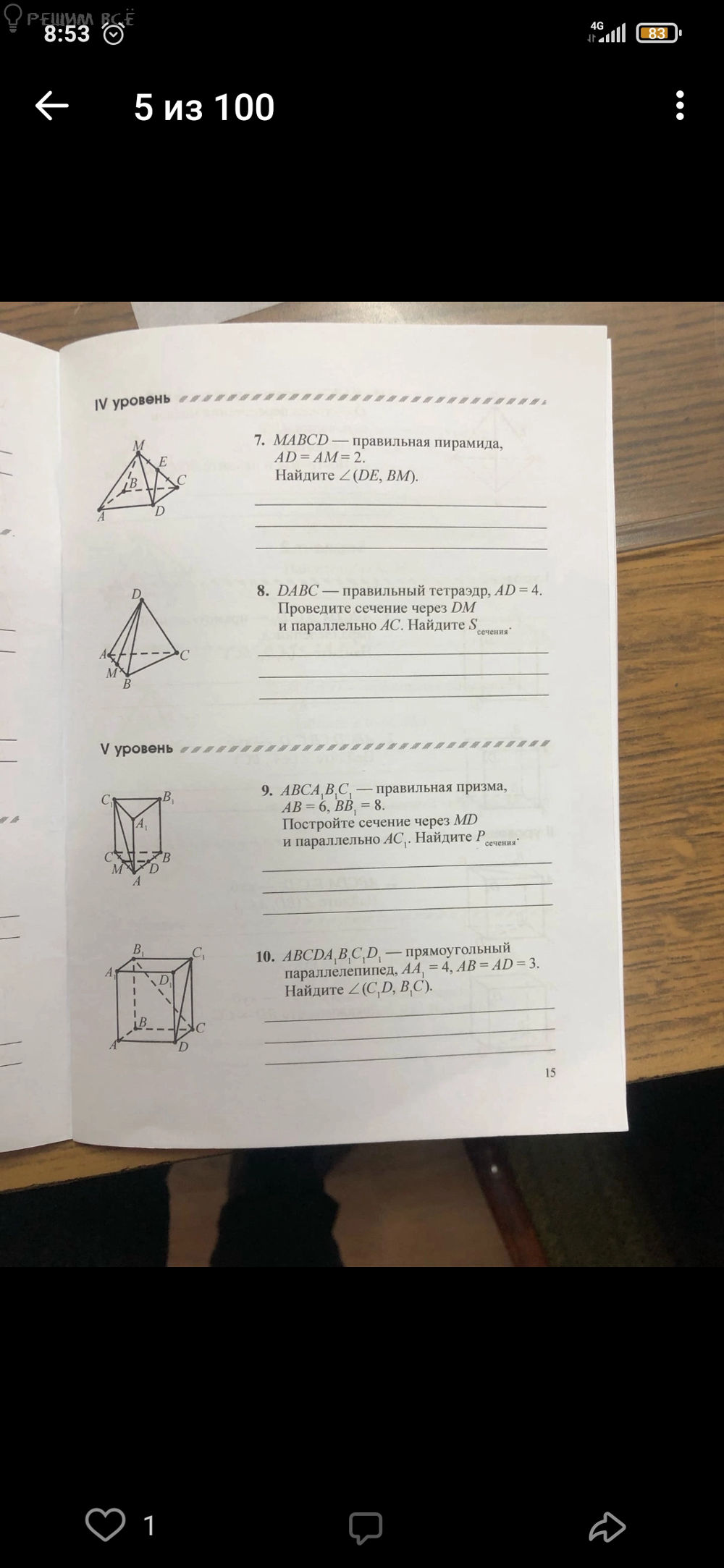
6. МАВСD — правильная пирамида. АВ = АМ. Найдите ∠(ТЕ, АМ).
7. МАВСD — правильная пирамида. АD = АМ = 2. Найдите ∠(DЕ, ВМ).
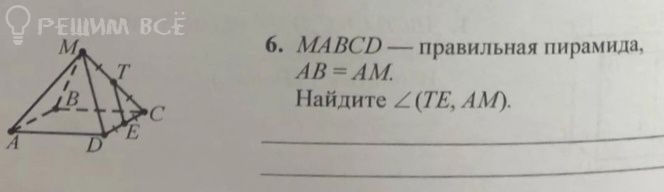

9. ΑВСDА1В1С1 — правильная призма, АВ = 6, ВВ1 = 8. Построить сечение через МD и параллельно АС. Найдите Рсечения.
10. ΑВСDА1В1С1D1 — призмоугольный параллелепипед, АС = 4, АВ = ΑD = 3. Найдите ∠(СD, ВС1).
Диагональ осевого сечения цилиндра равна 10 см, а угол между диагоналями осевого сечения, лежащего против диаметра основания, – 120°. Найдите площадь боковой поверхности цилиндра
У правильній трикутній призмі утворений переріз площиною, проведеною через сторону основи і середину протилежного бічного ребра. Обчисли площу перерізу, якщо сторона основи призми дорівнює 8 см, а висота призми дорівнює 14 см.
Основою піраміди є ромб, сторона якого дорівнює 32 см і гострий кут дорівнює 30°.
Усі кути, які утворюють бічні грані з площиною основи, дорівнюють60°.
Обчисли висоту і площу бічної поверхні піраміди.
Висота піраміди дорівнює
Площа бічної поверхні дорівнює
Основою прямого паралелепіпеда є ромб із гострим кутом 60° і більшою діагоналлю, що дорівнює 6 см, менша діагональ паралелепіпеда утворює з площиною основи кут 45°. Знайдіть площу бічної поверхні паралелепіпеда.
Шар вписан в цилиндр. Площадь поверхности шара равна 111. Найдите площадь полной поверхности цилиндра
Радиусы оснований шарового слоя равны 3 см и 4 см, радиус шара 5 см. Найдите объём слоя, если его основания расположены по одну сторону от центра шара
В нем нижнем основании цилиндра проведена хорда длиной 12см, которая находиться на расстоянии 5 см от центра этого основания. Высота цилиндра 7 см . Чему равен объём цилиндра
Длины сторон параллелепипеда составляют первые три члена геометрической последовательности. Их сумма равна 7, а объем параллелепипеда равен 8. Вычислите площадь полной поверхности.
Объём правильной четырёхугольной пирамиды 48, высота равна 4. Найдите площадь боковой поверхности пирамиды.
Найдите полную поверхность правильной усеченной четырехугольной пирамиды, стороны оснований которой равны 14 и 10, а диагональ равна 18.
основа прямої призми рівнобічна трапеція. Одна з основи у 2 рази більша за іншу, і кут при основі 45°, діагональ грані що містить меншу основу трапеції дорівнює 8 см і утворює кут 60° з площиною основи призми. Знайти об'єм
Помогите пожалуйста!!! В правильной треугольной призме АВСА1В1С1 проведено сечение СА1В, площадь которого составляет 4√35см².Косинус угла наклона диагонали боковой грани к основанию равен 1/3. Найдите объем призмы.
Объем правильной треугольной пирамиды равен 750. Через точку, делящую высоту этой пирамиды в отношении 2:3 (считая от вершины)параллельно основанию этой пирамиды проведено сечение. найдите объем части пирамиды, расположенной ниже этого сечения
Помогите пожалуйста!!! Срочно!В правильной треугольной
призме АВСА1В1С1 проведено сечение СА1В, площадь которого составляет 9√14см². Синус угла наклона диагонали боковой грани к основанию равен 1/3. Найдите объем призмы.
Варианты ответов:
1) 27√3 см³
2)48√3см³
3)27см³
4)54√3см³
5)54√2см³
Объём правильной четырехугольной пирамиды 48, высота равна 4. Найдите площадь боковой поверхности пирамиды.
В правильной треугольной пирамиде SABC с вершиной S проведена высота SO . На отрезке SO взята точка K так , что SK:KO=1:3 Известно, что боковые ребра образуют с основанием углы , равны π/6 , а расстояние от точки K до боковой грани состовляет 3/✓7. Найдите объем пирамиды
Осевое сечение конуса - правильный треугольник, площадь которого 4 корня из 3. вычислить объем конуса.
Площадь полной поверхности конуса равна 240. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.
Основою піраміди є квадрат зі стороною 8 см. Одне бічне ребро перпендикулярно площині основи і дорівнює 15 см.
Обчисли площу бічної поверхні.
Радиус цилиндра 8 см, высота 20 см. Найдите площадь его осевого сечения.
Дана прямая призма в основании которой равнобедренный треугольник. Боковая сторона основания равна 20 см, а высота – 16 см. Высота призмы – 10 см.
а) Вычислите площадь полной поверхности призмы.
б) Вычислите диагональ большей боковой грани.
Даний циліндр, площа бічної поверхні якого дорівнює 64πсм2.висота циліндра у два рази більша радіусу основи циліндра. Обчисли радіус основи циліндра
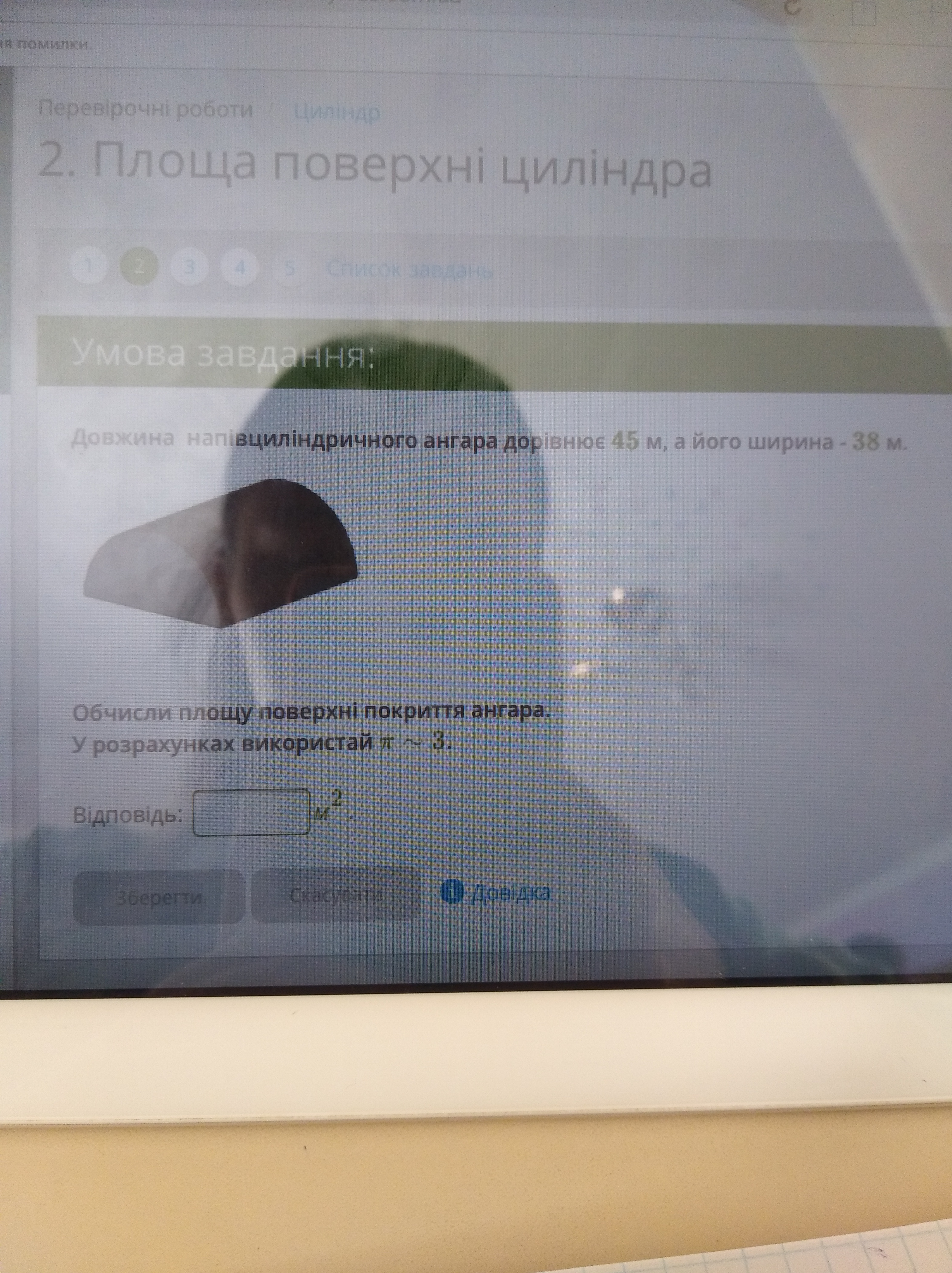
Довжина напівциліндричного Ангара дорівнює 45м, а його ширина 38м.Обчисли площу поверхні покриття Ангара. У розрахунках викорастай π ∼ 3
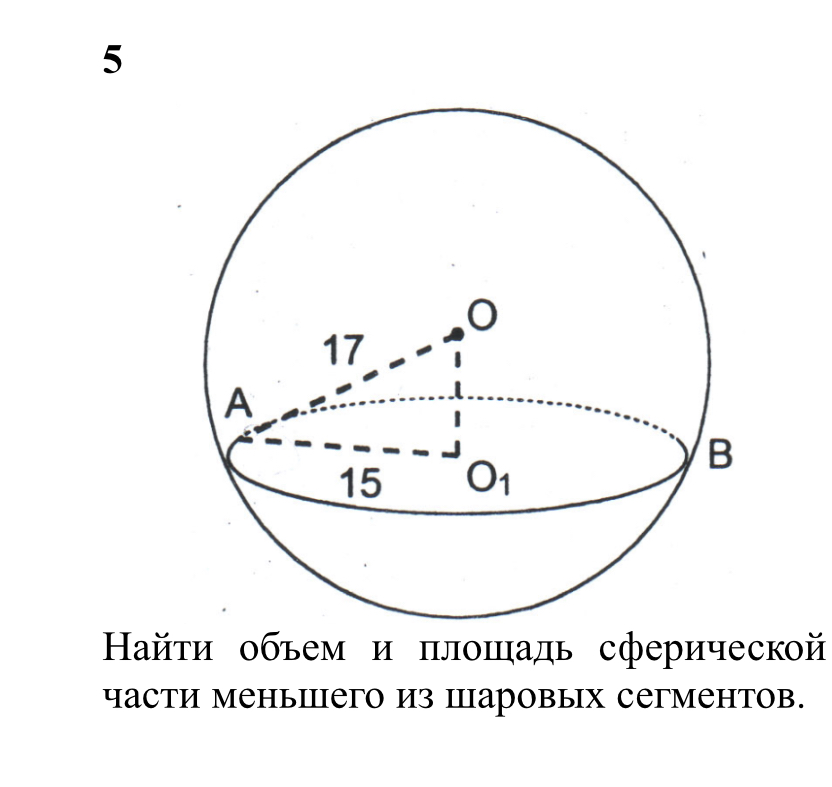
Найти объем и площадь сферической части меньшего из шаровых сегментов.
В прямоугольном параллелепипеде ABCDA1B1C1D, проведена секущая плоскость, содержащая диагональ АС1, и пересекающая рёбра ВВ1, и DD1, в точках F и Е соответственно.
а) Докажите, что сечение АFС1Е — параллелограмм.
б) Нейдите площадь сечения, если известно, что АFС1Е — ромб и АВ=3, BC=2, AA1=5.
1. Найдите площадь боковой поверхности правильной треугольной призмы, сторона
основы которой равна 3 см, а боковое ребро - 5 см.
2. Найдите объем прямой четырехугольной призмы, в основе которой лежит ромб с
диагоналями 12 см и 16 см, а боковое ребро - 10 см.
3. В правильной четырехугольной пирамиде высота равна 3 см, боковое ребро - 5см. Найдите объем пирамиды.
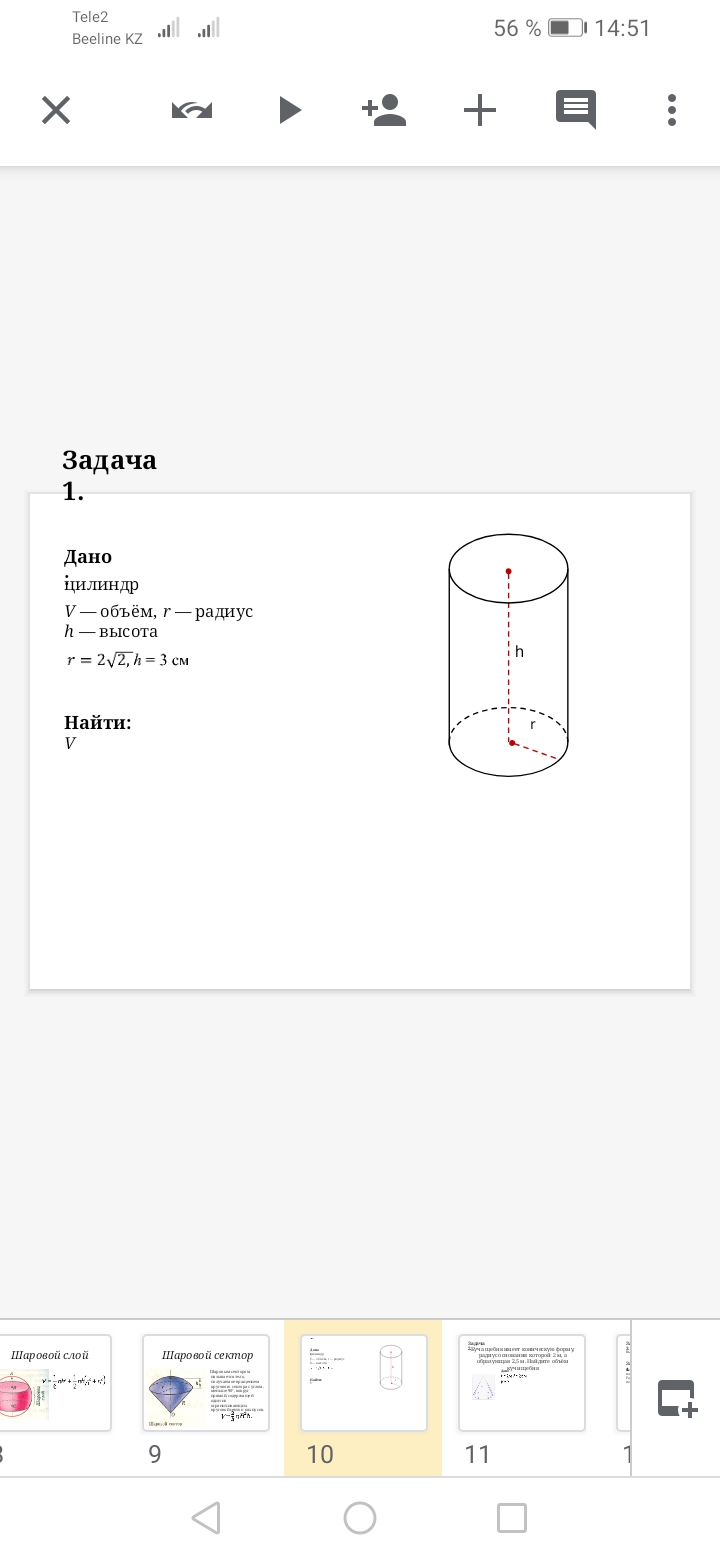
Задача 1.
Дано
цилиндр
V — объём, r — радиус
h — высота
r = 2√2, h = 3 см
Найти:
V
---
Задача 2.Куча щебня имеет коническую форму, радиус основания которой 2 м, а образующая 2,5 м. Найдите объём кучи щебня
Дано:
r = 2м l = 2,5м
V = ?
---
Задача 3.
Вычислите объём шара, если его радиус R=6 см.
Задача 4.
По разные стороны от центра шара проведены два параллельных сечения с площадями 9π см² и 16π см². Расстояние между сечениями равно 7 см. Определите объём получившегося шарового слоя.


Радиусы основания шарового слоя равны 9 см и 12 см ,а радиус шара -15 см. Чему равен объем шарового слоя, если параллельные плоскости, которые пересекают шар, расположены по одну сторону от его центра?
1) В основании прямой призмы лежит прямоугольный треугольник с катетами, равными 5 и 12. Высота призмы равна 8. Найдите полную поверхность призмы.
2) В правильной четырехугольной усеченной пирамиде стороны оснований 8 м и 2 м. Высота равна 4 м. Найдите полную поверхность.

Основание прямой призмы-прямоугольный треугольник с катетами 5 и 12 см. Вычислить площадь боковой и полной поверхности призмы если ее наибольшая боковая грань-квадрат
В основании прямой призмы лежит прямоугольный треугольник, один из катетов которого равен 4, а гипотенуза равна 4*sqrt(2). Найдите объём призмы, если её высота равна 3.
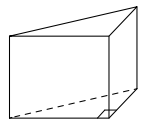
В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра призмы равны 6/Pi. Найдите объём цилиндра, описанного около этой призмы.
Вариант 4.
1. Площадь боковой поверхности правильной треугольной призмы равна 60см². Найдите боковое ребро призмы. Если сторона основания равна 5см.
2. Высота правильной четырехугольной призмы равна 11см, а сторона основания равна 2см. Найдите площадь боковой поверхности призмы и площадь полной поверхности призмы.
3. Найдите длину диагонали и площадь поверхности прямоугольного параллелепипеда, если его измерения равны 2см, 3см, 6см.
Вариант 3.
1. Найдите апофему правильной четырехугольной пирамиды, если ее высота равна 10см, а сторона основания 8см.
2. Апофема правильной треугольной пирамиды равна 4см и наклонена к плоскости основания под углом 60°. Найдите:
1) высоту пирамиды;
2) радиус окружности, вписанной в основание;
3) радиус окружности, описанной около основания;
4) сторону основания;
5) площадь основания;
6) площадь боковой грани;
7) площадь полной поверхности пирамиды;
8) Объем

длина основания правильной треугольной пирамиды 6 см,а двугранный угол у основания 60 градусов. Узнать площадь полной поверхности
Л8) Прямоугольник ABCD, у которого AB=4, AD=3, вращается вокруг прямой AD. Найдите площадь S поверхности тела вращения. В ответе укажите S/Pi.
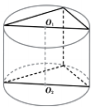
1) О - центр шара, вписанного в цилиндр, ABCD - осевое сечение цилиндра. Найти S_(бок.цил) / S_(сф)
1) Осевое сечение цилиндра квадрат, площадь которого равна 64см^2‚ Найдите радиус и высоту цилиндра.
2) Прямоугольник АВСО вращают через его меньшую сторону. Если площадь 60см° прямоугольника равна ‚а меньшая сторона 10 см, найдите площадь основания полученного цилиндра.
Осевое сечение цилиндра — квадрат, диагональ которого равна 6√2 см. Найдите площадь основания цилиндра.
Образующая конуса равна 10 см и образует с плоскостью основания угол 30°. Найдите площадь осевого сечения конуса.
Найдите площадь сечения шара радиуса 12 см плоскостью, находящейся на расстоянии 8 см от центра шара.
Образующая конуса равна 12 см. Найдите объем конуса, если диаметр его основания равен 12 см.
Площадь основания конуса равна 49π см², а его образующая — 9 см. Найдите боковую поверхность конуса.