Задача 65088 ...

62a895fd5211027240641e99

14.06.2022 17:09:25

В цилиндре
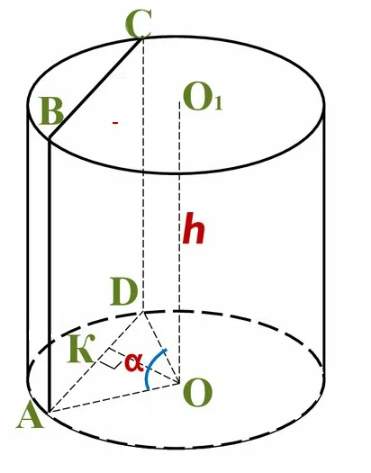
параллельно его оси
проведена плоскость,
пересекающая нижнее
основание цилиндра по
хорде, которую видно
из центра этого
основания под углом α.
Найдите площадь
боковой поверхности
цилиндра, если площадь
образовавшегося
сечения равна S.

5f3ea7e3faf909182968ddd9

14.06.2022 21:24:05

★

AD=2 AK

AK=R*sin( α /2)

AD=2*R*sin( α /2)

S_(ABCD)=S

S_(ABCD)=AD*h=2*R*h*sin (α /2)

2*R*h*sin (α /2)=[b]S[/b] ⇒

R*h=[b]S/(2sin(α /2))[/b]



S_(бок. пов)=2π*R*h=2π*([b]S/(2sin(α /2))[/b])=πS/sin (α /2)