Задача 28378 ...
Условие
1. Площадь боковой поверхности правильной треугольной призмы равна 60см². Найдите боковое ребро призмы. Если сторона основания равна 5см.
2. Высота правильной четырехугольной призмы равна 11см, а сторона основания равна 2см. Найдите площадь боковой поверхности призмы и площадь полной поверхности призмы.
3. Найдите длину диагонали и площадь поверхности прямоугольного параллелепипеда, если его измерения равны 2см, 3см, 6см.
Вариант 3.
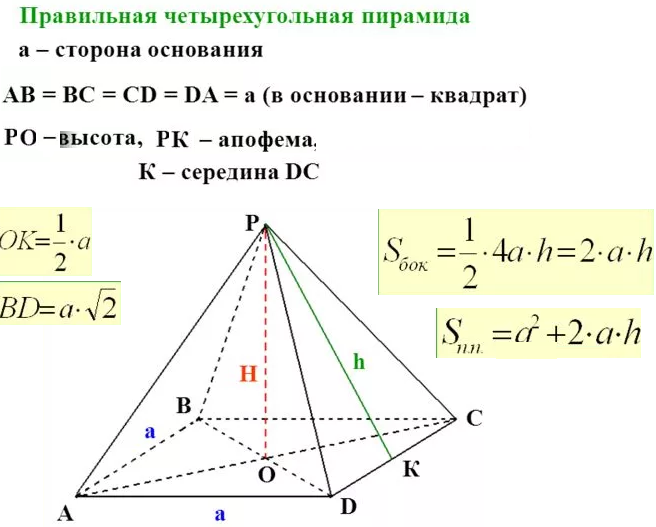
1. Найдите апофему правильной четырехугольной пирамиды, если ее высота равна 10см, а сторона основания 8см.
2. Апофема правильной треугольной пирамиды равна 4см и наклонена к плоскости основания под углом 60°. Найдите:
1) высоту пирамиды;
2) радиус окружности, вписанной в основание;
3) радиус окружности, описанной около основания;
4) сторону основания;
5) площадь основания;
6) площадь боковой грани;
7) площадь полной поверхности пирамиды;
8) Объем
Все решения
S(бок)=P(осн.)*H
60=15*H
H=4
H = боковому ребру
О т в е т. 4
2.
S(бок)=P(осн)*Н=(2+2+2+2)*11=88
S(полн.)=S(бок.)+2S(осн.)=88+2*2^2=96
3.
d^2=a^2+b^2+c^2=2^2+3^2+6^2=4+9+36=49
d=7
S( пов.)=2ab+2bc+2ac=2*2*3+2*2*6+2*3*6=72
4. см. рис.
h^2=H^2+(a/2)^2=10^2+4^2=116
h=sqrt(116)
5. см. рис.
h=4
∠ РKО= 60 градусов
а)PO=H=4*sin60 градусов=2sqrt(3) - высота пирамиды
б)(1/2)a=4*cos30^(o)=4*(1/2)=2
r=a/2=2
a=4
в)
d^2=a^2+a^2=462+4^2=32
d=AC=BD=4sqrt(2)
R=АО=ОС=ОB=OD=(1/2)АС=(1/2)BD=2sqrt(2)
г) а=4
д)S( осн)=a^2=4^2=16
е) S=(1/2)a*h=(1/2)4*4=9
ж)V=(1/3)S(осн.)*Н=(1/3)*4^2*2sqrt(3)=32sqrt(3)/3