Задача 57580 ...

60084f73a8b7045a0a52d6e1

31.01.2021 17:54:44

Помогите пожалуйста!!! Срочно!В правильной треугольной
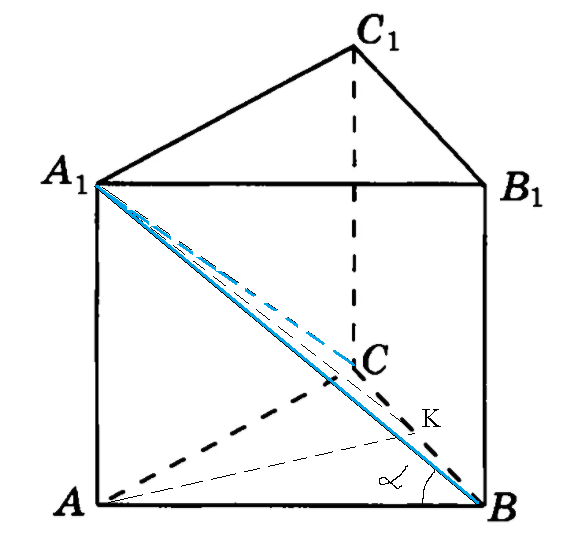
призме АВСА1В1С1 проведено сечение СА1В, площадь которого составляет 9√14см². Синус угла наклона диагонали боковой грани к основанию равен 1/3. Найдите объем призмы.
Варианты ответов:
1) 27√3 см³
2)48√3см³
3)27см³
4)54√3см³
5)54√2см³

5f3ea7e3faf909182968ddd9

01.02.2021 09:11:50

★

АВСА_(1)В_(1)С_(1) - правильная пирамида
AB=BC=AC
AA_(1) ⊥ пл. АВС; ВВ_(1) ⊥ пл. АВС; СС_(1)⊥ пл. АВС.

sin ∠ A_(1)BA=1/3

sin ∠ A_(1)BA=AA_(1)/A_(1)B ⇒ A_(1)B =[b]3AA_(1)[/b]

Тогда изз Δ A_(1)BA
АB^2=A_(1)B^2-AA_(1)^2=([b]3AA_(1)[/b])^2-([b]AA_(1)[/b])^2=8([b]AA_(1)[/b])^2

[b]H_(призмы)=АА_(1)[/b]

[b]AB=a=AA_(1)*sqrt(8)[/b]

Из Δ A_(1)KB

A_(1)K^2=А_(1)B^2-AK^2=([b]3AA_(1)[/b])^2)^2-([b]AA_(1)*sqrt(8)[/b]/2)^2=9*(AA_(1))^2-2(AA_(1))^2=7(AA_(1))^2


A_(1)K=sqrt(7)([b]AA_(1)[/b])


S_( Δ А_(1)BC)=(1/2)BC*A_(1)K=(1/2)*(AA_(1)*sqrt(8))*sqrt(7)([b]AA_(1)[/b])

По условию:

S_( Δ А_(1)BC)=9sqrt(14)

Из уравнения:

(1/2)*(AA_(1)*sqrt(8))*sqrt(7)([b]AA_(1)[/b])=9sqrt(14)

(AA_(1))^2=9

AA_(1)=3


[b]H_(призмы)=АА_(1)=3[/b]

[b]AB=a=AA_(1)*sqrt(8)=3sqrt(8)=6sqrt(2)[/b]

V=S_(осн)*H=(1/2)a^2*sin60 ° *H=(1/2)*(6sqrt(2))^2*(sqrt(3)/2)* 3=[b]54sqrt(3)[/b]