Задача 73214 ЗАДАЧА No3 У тетраедрі ОАВС з вершини О...

6523cac29d4b23649aa5898c

09.10.2023 12:44:33

ЗАДАЧА No3
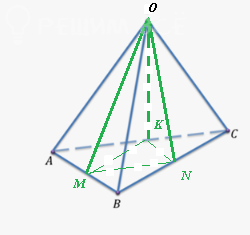
У тетраедрі ОАВС з вершини О проведені медіани бічних граней.Беручи їх за ребра нового тетраедра, довести, що об’єм його становить 0,25 об’єму тетраедра ОАВС.

5f3ea7e3faf909182968ddd9

09.10.2023 12:59:22

★

V_(OABC)=[b](1/3)S_( Δ ABC) * H[/b]

M- середина АВ
N- середина ВС
К- середина АС

Δ MNK ∼ Δ АВС k=1/2

S_( Δ MNK) : S_( Δ ABC)=1:4

V_(OMNK)=(1/3)S_( Δ MNK) * H

V=[b](1/3)[/b]*(1/4)*[b]S_( Δ ABC)*H[/b]=(1/4) *V_(OABC)=0,25*V_(OABC)