Задача 56405 ...

5fe230dd1c6d1142ab516492

22.12.2020 20:46:43

В правильной треугольной пирамиде SABC с вершиной S проведена высота SO . На отрезке SO взята точка K так , что SK:KO=1:3 Известно, что боковые ребра образуют с основанием углы , равны π/6 , а расстояние от точки K до боковой грани состовляет 3/✓7. Найдите объем пирамиды

5f3ea7e3faf909182968ddd9

22.12.2020 21:17:15

★

KD=3/sqrt(7)

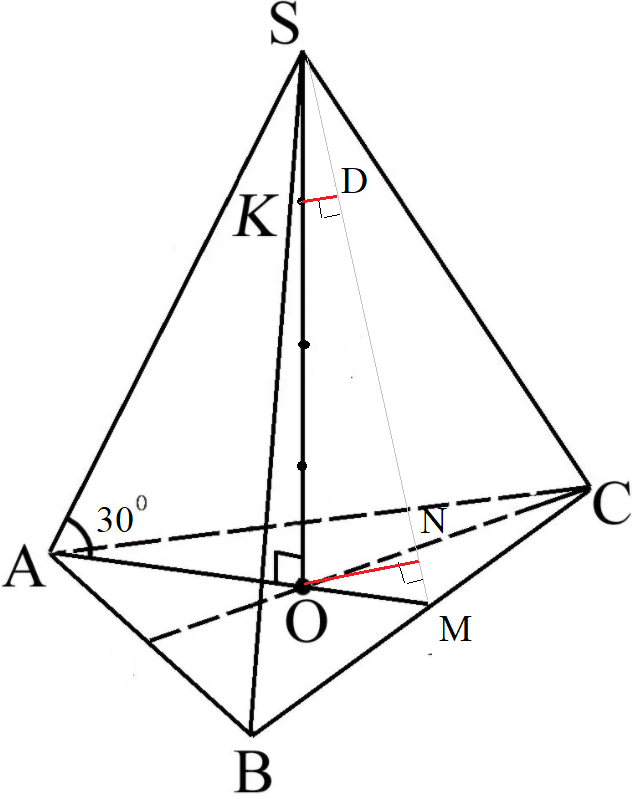
Δ SKD ∼ Δ SON c коэффициентом подобия 1:4 ( SK:KO=1:3 ⇒ SK:SO=1:4)

ON=12/sqrt(7)


Пусть AB=BC=AC=a

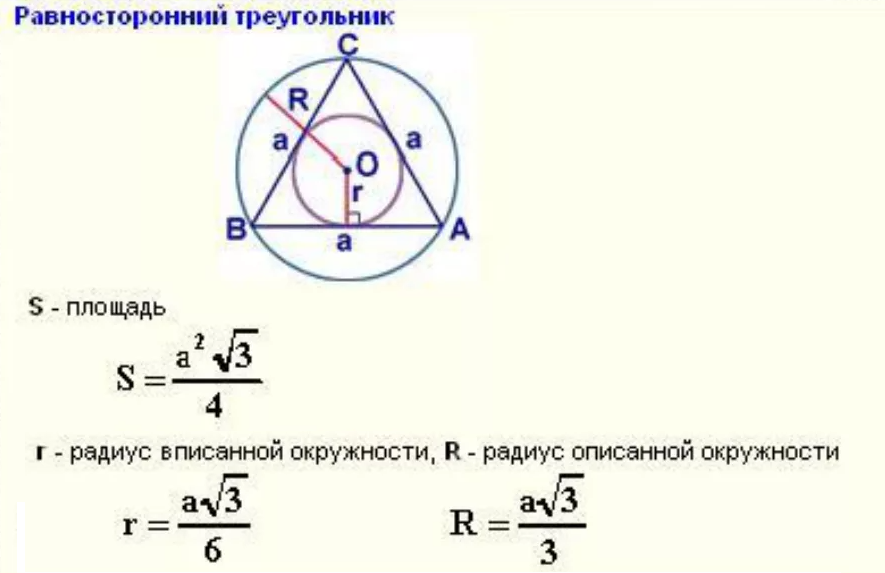
AO=asqrt(3)/3 ( cм скрин)

OM=asqrt(3)/6

SO=AO*tg30 ° =asqrt(3)/3*(sqrt(3)/3)=a/3

SM^2=SO^2+OM^2=(a/3)^2+(asqrt(3)/6)^2

SM=a*sqrt(7)/6

SO*OM=SM*ON

(a/3)*(a*sqrt(3)/6)=(a*sqrt(7)/6)*(12/sqrt(7)) ⇒


a=

V=(1/3)S_(осн)*SO=(1/3)*(a^2sqrt(3)/4)*(a/3)=...