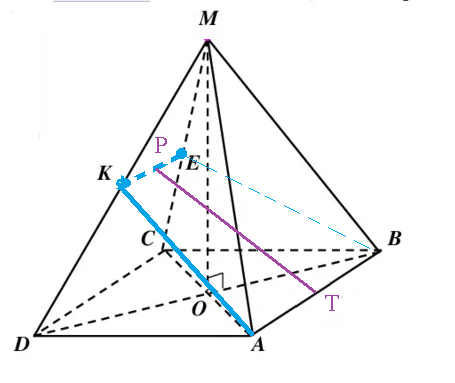
Задача 63614 B основании пирамиды МABCD...

622af82ec21b025300be8657

11.03.2022 10:21:54

B основании пирамиды МABCD параллелограмм ABCD. В каком отношении, считая от вершины, делит объем пирамиды сечение, проходящее через ребро АВ и середину реб pa MC?

5f3ea7e3faf909182968ddd9

11.03.2022 13:33:59

★

Сечение - трапеция АВEK

V=V_(МАBСD)=(1/3)S_(параллелограмма АВСD)*SO

V_(1)=V_(МАBKE)=(1/3)S_(трапеции АВEK)*MP

V_(2)=V-V_(1)

Найти

V_(1)/V_(2)=?