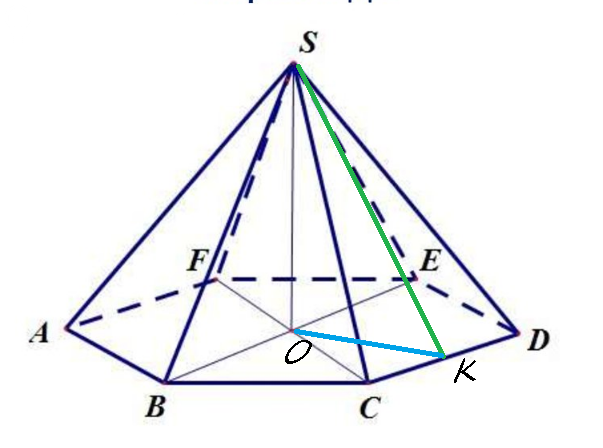
Задача 70037 Задана правильная шестиугольная...

640f52950e63823cebb2f376

13.03.2023 19:44:12

Задана правильная шестиугольная пирамида, высота которой равна 8. Угол между высотой и апофемой пирамиды равен 60°.

Определите длину стороны основания пирамиды (12 баллов).
Определите длину бокового ребра пирамиды (10 баллов).
Вычислите объём пирамиды (10 баллов).

5f3ea7e3faf909182968ddd9

13.03.2023 20:26:40

★

SO=8

SK ⊥ CD
SK - [i]апофема боковой грани[/i]

∠ ОSK=60 °
SO ⊥ пл ABCDEF ⇒ SO ⊥ OK
Δ ОSK - [i]прямоугольный[/i]
∠ ОKS=30 °
SK=16 ( катет SO против угла в 30 ° равен половине гипотенузы, значит гипотенуза в 2 раза больше катета SO)
[i]апофема боковой грани[/i] равна 16

OK^2=SK^2-SO^2=16^2-8^2=(16-8)*(16+8)=8*24=8*8*3

[b]OK=8*sqrt(3)[/b]

ABCDEF - правильный шестиугольник ⇒ Δ COD - равносторонний треугольник

OK - высота равностороннего треугольника

h=a*sqrt(3)/2 ⇒ a=2h/sqrt(3)=2*8sqrt(3)/sqrt(3)=16

a=16 - [b]сторона шестиугольника[/b]

OC=CD=16

По теореме Пифагора из прямоугольного треугольника SOC

SC^2=SO^2+OC^2=8^2+16^2=64+256=320
SC=sqrt(320)=sqrt(64*5)=[red]8*sqrt(5)[/red]


V_(пирамиды)=(1/3)*S_(осн)*Н=(1/3)*6*[blue]S_( Δ COD)[/blue]*H=(1/3)*6*[blue](16^2sqrt(3)/4)[/blue]*8=1024sqrt(3)