Задача 62495 ...
Условие
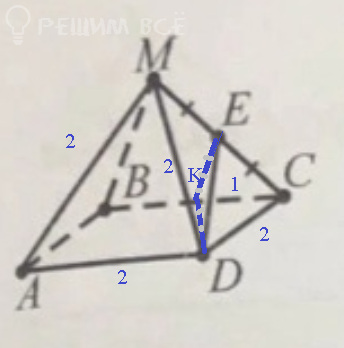
7. МАВСD — правильная пирамида. АD = АМ = 2. Найдите ∠(DЕ, ВМ).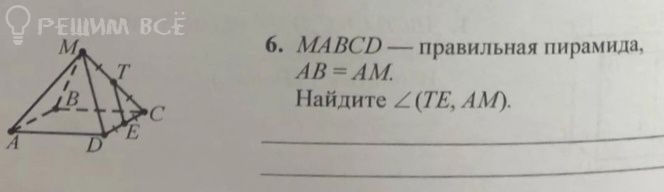

математика колледж
1267
Решение
★
TE|| MD
∠ (TE,AM)= ∠ MD, AM)= ∠ AMD=60 ° ,
Δ AMD - равносторонний.
7.
Проводим EK || BM
EK- средняя линия Δ ВМС
EK=(1/2)BM=1
∠ (DE,BM)= ∠ (DE,EK)= ∠ DEK
Находим стороны Δ DEK:
EK=1
Из равностороннего Δ MDC
DE- медиана, а значит и высота
По теореме Пифагора
DE^2=DC^2-C^2=2^2-1^2=3
DE=sqrt(3)
Из равностороннего Δ KDC по теореме Пифагора:
KD=sqrt(1^2+2^2)=sqrt(5)
По теореме косинусов:
KD^2=KE^2+ED^2-2*KE*ED*cos∠ DEK
(sqrt(5))^2=1^2+(sqrt(3))^2-2*1*sqrt(3)*cos∠ DEK ⇒ cos∠ DEK=[b]1/2sqrt(3)[/b]