Задача 77418 3. Основание АВС правильной пирамиды...

663d319f28a0db7674c079f8

5/9/2024 8:27:52 PM

3. Основание АВС правильной пирамиды АВСD лежит в плоскости Оху, известны координаты вершин А и В: A(1; 0; 0) B(- 1; 0; 0)

Найдите координаты остальных вершин пирамиды, учитывая, что AB = BD Рассмотрите все случаи.

5f3ea7e3faf909182968ddd9

5/10/2024 6:43:42 AM

★

A(1; 0; 0) B(– 1; 0; 0)

Тогда


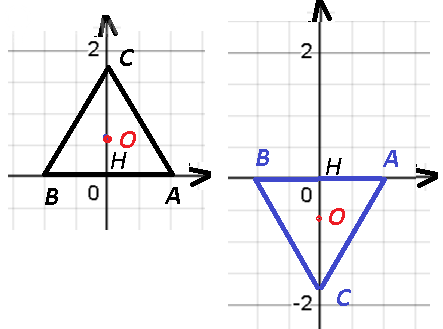
A(1; 0; 0) B(– 1; 0; 0)

Так как основание ABC - это равносторонний треугольник, то вершина С находится на середине оси Оу, и ее координаты будут равны
С(0; [b]y[/b]; 0)
или
С(0; -[b]y[/b]; 0),

Так как AB=2
найдем координату [b]y[/b] по теореме Пифагора из треугольника АСН

( СН ⊥ АВ)

СH^2 =(AC^2 - AH^2) =2^2-1^2=3

CН=3

y= ± 3

1)
случай
С(0; [b]sqrt(3)[/b]; 0)

Точка O - центр правильного треугольника АВС

( точка пересечения его медиан и биссектрис и высот, центр вписанной и описанной окружностей)

СO:OH=2:1

O(0;sqrt(3)/3; 0)

D(0;sqrt(3)/3; z)

AB = BD

BO=CO=(2/3)sqrt(3)


DO^2=BD^2-BO^2=2^2-(2sqrt(3)/3)^2=4-(4/3)=8/3

DO=2sqrt(2/3)

D(0;sqrt(3)/3;2sqrt(2/3))


Ответ:

a)
С(0; [b]sqrt(3)[/b]; 0)
D(0;sqrt(3)/3;2sqrt(2/3))

б)
С(0; [b]-sqrt(3)[/b]; 0)
D(0;-sqrt(3)/3;2sqrt(2/3))