Задача 68583 Задание 6. Найти угол между прямой А1В и...
Условие
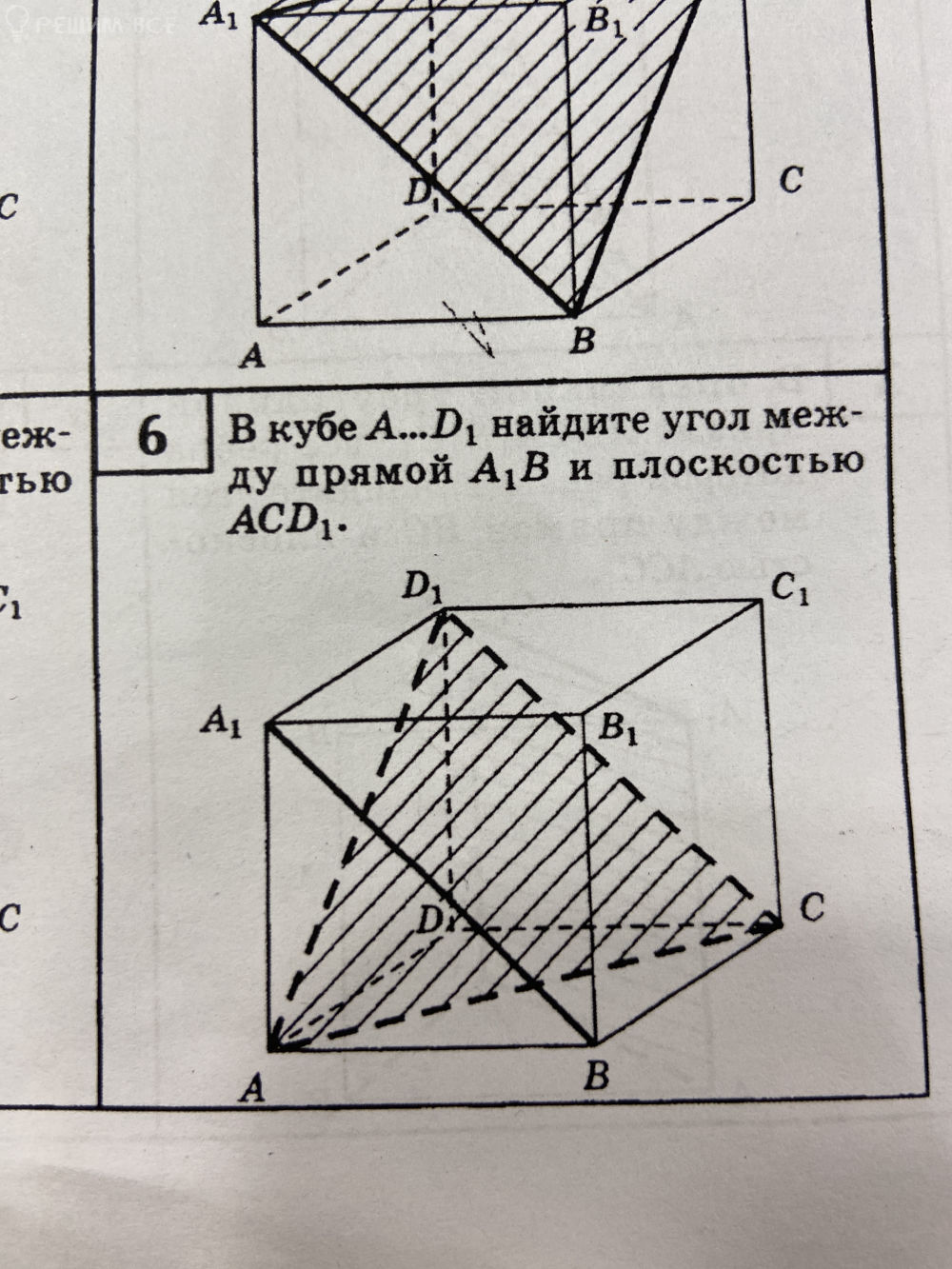
Решение
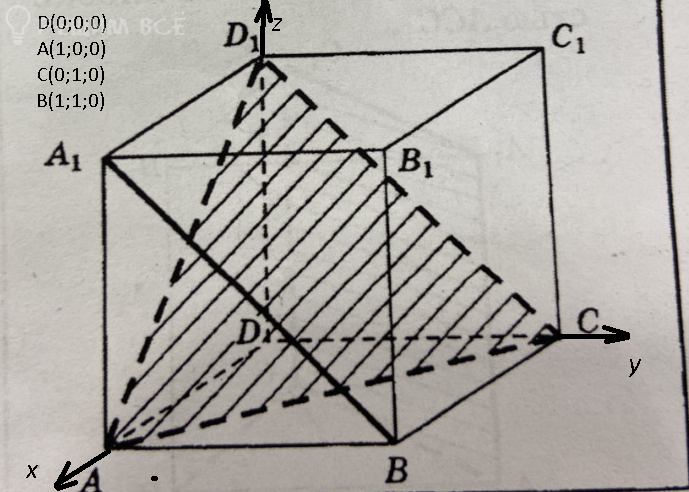
D(0;0;0)
A(1;0;0)
C(0;1;0)
B(1;1;0)
D_(1)(0;0;1)
A_(1)(1;0;1)
C_(1)(0;1;1)
B_(1)(1;1;1)
Составляем уравнение плоскости AD_(1)C:
ax+by+cz+d=0
A(1;0;0)
[b]a*1+d=0[/b] ⇒ a=-d
C(0;1;0)
[b]b*1+d=0[/b] ⇒ b=-d
D_(1)(0;0;1)
[b]c*1+d=0[/b] ⇒ c=-d
-dx-dy-dz+d=0
[b]x+y+z-1=0[/b]
нормальный вектор плоскости vector{n}=(1;1;1)
vector{A_(1)B}=(1-1;1-0;0-1)=(0;1;-1)
vector{n}=(1;1;1)
vector{A_(1)B}=(0;1;-1)
vector{n}*vector{A_(1)В}=1*0+1*1+1*(-1)=0
Скалярное произведение векторов равно 0
Векторы vector{n} и vector{A_(1)В} [b]ортогональны[/b]
Угол между прямой и плоскостью - это дополнительный угол ( см. объяснение на скрине)
поэтому прямая и плоскость [b]параллельны[/b]