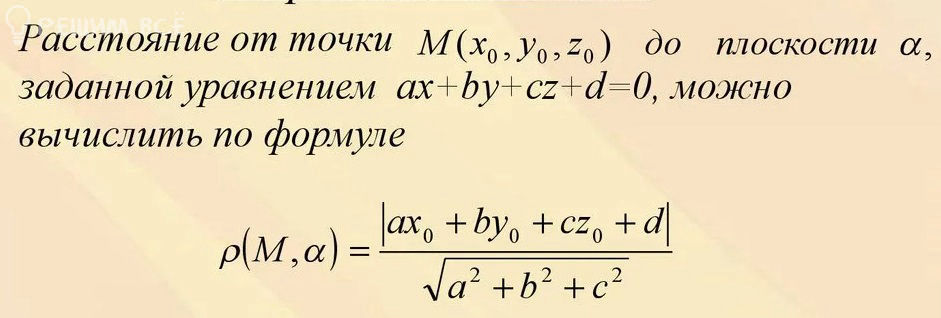Задача 77094 Задача 11. В правильной четырехугольной...
Условие
Задача 11. В правильной четырехугольной призме ABCDA1 B1C1D1 со стороной основания 4 и высотой 7 на ребре АА1 взята точка М так, что АМ=2. На ребре ВВ1 взята точка К так, что
В1К=2. Найдите угол между плоскостью, проходящей через точки D1, M, К и плоскостью СС1D1, расстояние от точки В1 до плоскости D1MK.
Решение
А(0;0;0)
ось Ох - по отрезку ФВ
ось Оу - по отрезку АВ
ось Оz - по отрезку АА_(1)
А(0;0;0) ; M (2;0;0)
D(4;0;0) ; D_(1)(4;0;7)
B(0;4;0); K(0;4;5)
Составим уравнение плоскости АКD_(1) в виде
ax+by+cz+d=0
Подставляем координаты точек
M (0;0;2)
a*0+b*0+c*2+d=0 ⇒ с=- (d/2)
D_(1)(4;0;7)
a*4+b*0+c*7+d=0 ⇒ a*4+7*(-d/2)+d=0 ⇒ a=5d/8
K(0;4;5)
a*0+b*4+c*5+d=0 ⇒ 4b+5*(-d/2)+d=0⇒ b=3d/8
Уравнение плоскости принимает вид:
(5d/8)*x+(3d/8)*y+(-d/2)*z+d=0
Делим на d
(5/8)x+(3/8)y-(1/2)z+1=0
или
[b]5x+3y-4z+8=0[/b]
vector{n_(MKD_(1))}=(5;3;-4)
vector{n_(CDD_(1))}=vector{i}=(1;0;0)
Угол между плоскостями найдем как угол между нормальными векторами
cos φ =(5*1+3*0+(-4)*0)/sqrt(5^2+3^2+(-4)^2)=5/sqrt(50)=1/sqrt(2)
⇒ φ =π/4
б)
Расстояние от точки B_(1)(0;4;7)до плоскости по формуле:
d=(|5*0+3*4+(-4)*7+8)/sqrt((5^2+3^2+(-4)^2)=8/sqrt(50)=8/(5*sqrt(2))=[b]4sqrt(2)/5[/b]