Задача 61885 для прямоугольного параллелепипеда...

619e48df21b169759d75fdaa

30.11.2021 05:24:45

для прямоугольного параллелепипеда ABCDA1B1C1D1, у которого AB=2, AD=2, AA1=1, найдите расстояние от вершины A1 до плоскости ACD1

5f3ea7e3faf909182968ddd9

30.11.2021 12:18:36

★

1 способ. Проводим перпендикуляр на плоскость АСD_(1)

A_(1)K ⊥ AD_(1)


A_(1)K=S_( Δ AA_(1)D)/AD_(1)=1*2/sqrt(5)=[red][b]2sqrt(5)/5[/b][/red]


2 способ Координатный.

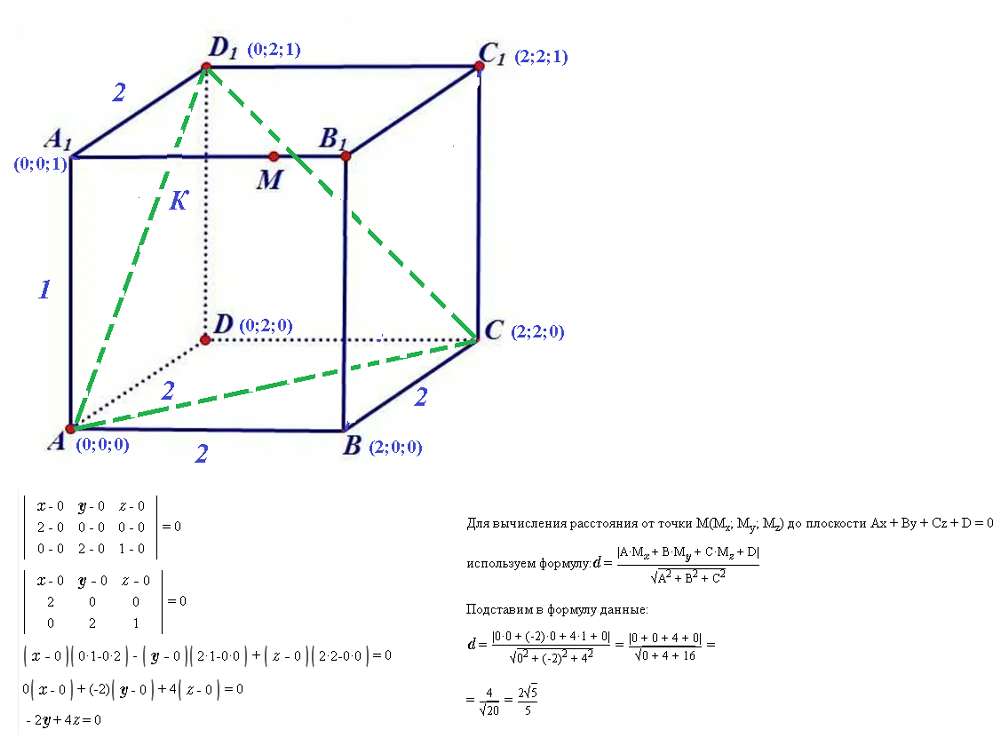
Располагаем систему координат в пространстве так, чтобы точка А совпадала с началом координат (0;0;0)

Ось Ох совпадала с лучом AB

ОСь Оу совпадала с лучом AD

Координаты остальных точек на рисунке.

Составляем уравнение плоскости, проходящей через три точки:

ax+by+cz=0

Подставляем координаты точек А; С и D_(1)

Получаем уравнение: [m] -2y+4z=0[/m]

Тогда расстояние от точки А_(1) до плоскости находим по формуле.