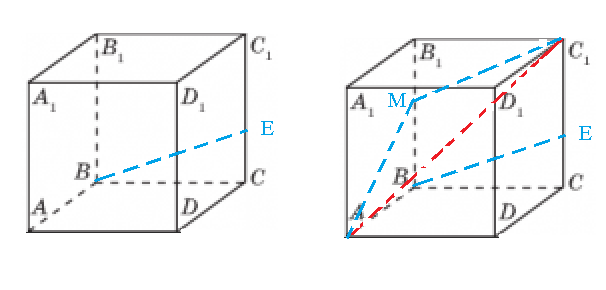
Задача 59645 На ребре СС1 куба ABCDA1B1C1D1 отмечена...

6098d421948cd266b38ecf4b

10.05.2021 09:49:15

На ребре СС1 куба ABCDA1B1C1D1 отмечена точка Е так, что СЕ:ЕС1=1:2. Найдите угол между прямыми ВЕ и АС1

5f3ea7e3faf909182968ddd9

10.05.2021 10:07:47

★

MC_(1)|| BE
M ∈ BB_(1)
B_(1)M:MB=1:2

∠ MC_(1)A находим из Δ АМС_(1) по теореме косинусов

Пусть ребро куба равно 1

B_(1)M=СЕ=1/3
MB=ЕС_(1)=2/3


Находим

AM=sqrt(1^2+(2/3)^2)=sqrt(13)/3
MC_(1)=BE=sqrt(1+(1/3)^2)=sqrt(10)/3
AC_(1)=sqrt(3)

АМ^2=AC^2_(1)+MC^2_(1)-2*AC_(1)*MC_(1)*cos ∠ MC_(1)A

(13/9)=3+(10/9)-2*sqrt(3)*(sqrt(10)/3)cos ∠ MC_(1)A ⇒

cos ∠ MC_(1)A=(24/9)/2*(sqrt(10/3))=[b]4/sqrt(30)[/b]