Задача 56085 В основе пирамиды лежит равносторонний...

5f6cf18a347ae046112d5363

11.12.2020 17:41:40

В основе пирамиды лежит равносторонний треугольник с основанием 6 см и высотой 9 см. Все стороны пирамиды равны 13 см. Вычислите высоту этой пирамиды.

5f3ea7e3faf909182968ddd9

11.12.2020 22:19:31

★

Все боковые ребра пирамиды равны 13 см.

Равные наклонные имеют равные проекции

Значит высота пирамиды проектируется в центр описанной окружности.

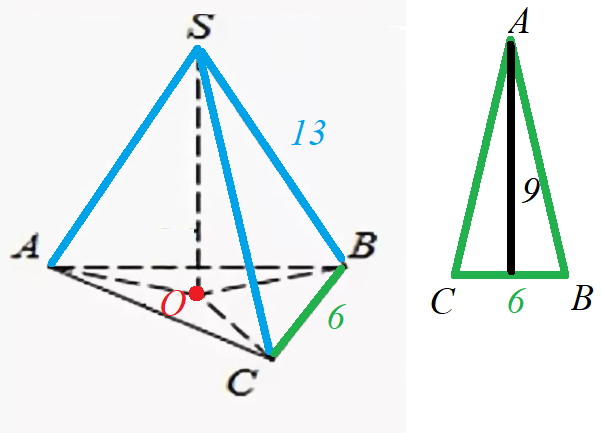
Имеем задачу планиметрии. Дан равнобедренный треугольник, основание - 6, высота - 9.

Найти радиус описанной окружности.

По формуле R=abc/4S

S=(1/2)*a*h=(1/2)*6*9=27

b=c=sqrt(9^2+3^2)=sqrt(81+9)=sqrt(90)=3sqrt(10)

Вычислите высоту этой пирамиды.

R=6*(3sqrt(10)*3*sqrt(10))/(4*27)=5

H^2=13^2-5^2=169-25=144

H=12