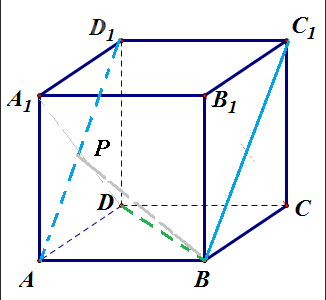
Задача 63223 дан куб ABCDA1B1C1D1 найдите угол между...
Условие
Решение
Так как плоскость ABC1 пересекает параллельные плоскости - основания куба АВСD и АВСD -
по параллельным прямым, то такие прямые это АВ и C_(1)D_(1)
Значит плоскость ABC1 - это плоскость АВС_(1)D_(1)
Угол между прямой и плоскостью - угол между прямой и ее проекцией на плоскость
Проводим A_(1)D
Диагонали квадрата АА_(1)D_(1)D взаимно перпендикулярны
DP ⊥ AD_(1)
AB ⊥ пл АА_(1)D_(1)D ⇒ AB ⊥ DP
DP ⊥ двум пересекающимся прямым AD_(1) и AB плоскости АВС_(1)D_(1) ⇒ DP ⊥ плоскости АВС_(1)D_(1)
BP - проекция BD на плоскости АВС_(1)D_(1)
∠ DBP - угол между прямой BD и плоскостью АВС_(1)D_(1)
Находим его из прямоугольного треугольника BDP
BD=sqrt(2)
DP=sqrt(2)/2
cos ∠ DBP =DP/BD=1/2
∠ DBP =60 °