Задача 64582 ...
Условие
а)определите, какой угол является углом между плоскостями ABC и ACD,и докажите это
Б) найдете градусную меру этого угла 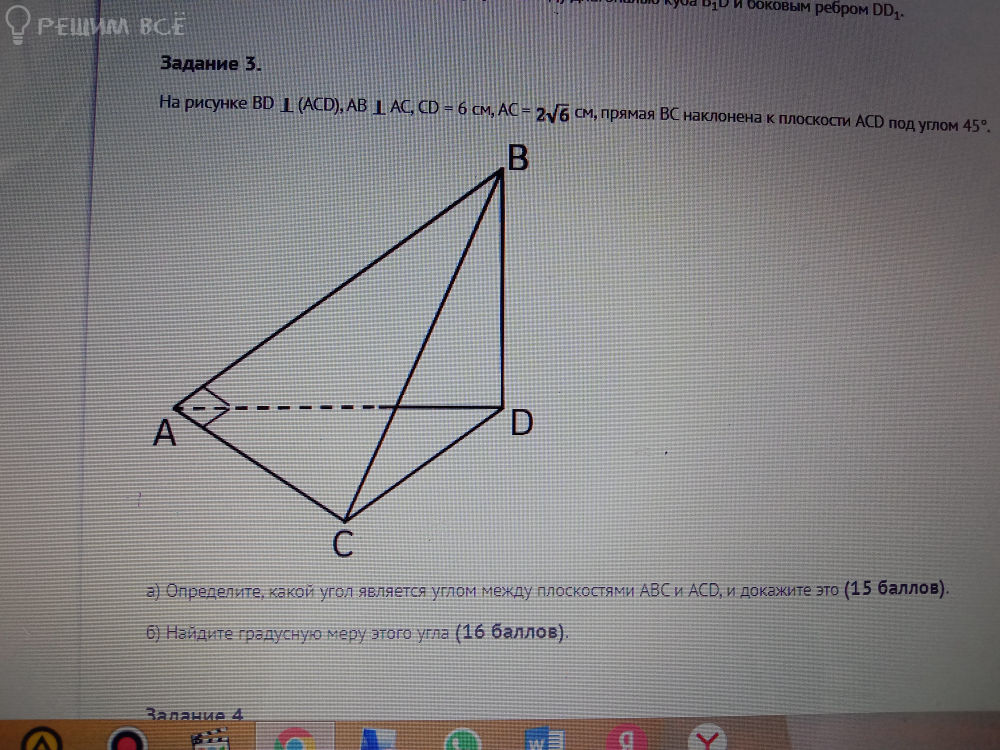
Решение
АB- наклонная
AD- проекция
AB ⊥ AC ⇒ по т. о трех перпендикулярах
AD⊥ AC
[b]∠ BAD[/b] - линейный угол двугранного угла, образованного плоскостями ABC и ACD
AD⊥ AC ⇒ ∠ DAC=90 °
Δ DAC прямоугольный, по теореме Пифагора
СD^2=AD^2+AC^2
По условию:
CD=6 см
AC=2√6см
AD^2=6^2-(2√6)^2=36-24=12
[b]AD=2sqrt(3)[/b]
По условию:
прямая BC наклонена к плоскости ACD под углом 45 ° ⇒ Δ BCD - [i]прямоугольный равнобедренный[/i], так как ∠ BCD=45 °
СD=BD=6 см
Из прямоугольного треугольника BAD:
tg ∠ BAD=BD/AD=6/2sqrt(3)=sqrt(3)
∠ BAD=60 °