Задача 60436 Тангенс угла между боковыми гранями...
Условие
Решение
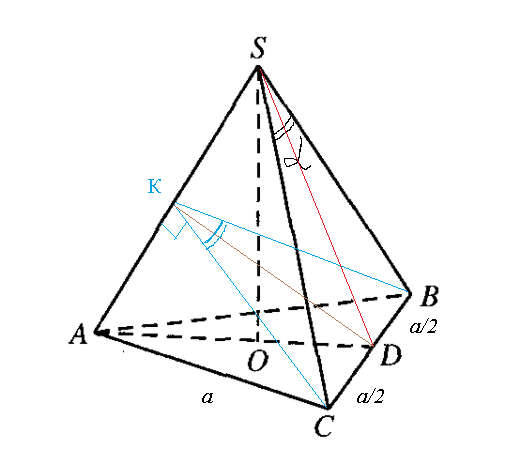
∠ ВКС - линейный угол двугранного угла
tg ∠ BKC=[m]2\sqrt{2}[/m]
Пусть плоский угол при вершине [m]α [/m]
Выразим тригонометрические функции ∠ BKC через тригонометрические функции угла [m]α [/m]
Обозначим сторону основания пирамиды через [m]a[/m] ,
Находим
[m]SD=\frac{CD}{tg\frac{α}{2}}=CD\cdot ctg\frac{α}{2} =\frac{a}{2}\cdot ctg\frac{α}{2}[/m]
[m]SC=\frac{CD}{sin\frac{α}{2}}=\frac{a}{2sin\frac{α}{2}}[/m]
S_( Δ SBC)=[m]\frac{1}{2}BC\cdot SD=\frac{1}{2}\cdot a\cdot \frac{a}{2}\cdot ctg\frac{α}{2}=\frac{a^2}{4}\cdot ctg\frac{α}{2}[/m]
S_( Δ SAC)=S_( Δ SBC)=S_( Δ SAB)
SA=SB=SC
Так как с другой сторона
S_( Δ SAC)=[m]\frac{1}{2}SA\cdot KC[/m], то
KC=[m]\frac{2S_{ Δ SAC}}{SA}=\frac{2\cdot \frac{a^2}{4}\cdot ctg\frac{α}{2}}{\frac{a}{2sin\frac{α}{2}}}=actg\frac{α}{2}\cdot sin\frac{α}{2}=a\cdot cos\frac{ α}{2} [/m]
Из Δ СDK
sin [m]\frac{ ∠ BKC}{2}=\frac{CD}{KC}=\frac{\frac{a}{2}}{a cos\frac{α}{2}}=\frac{1}{2cos\frac{α}{2}}[/m]
Итак, получена связь между синусом половинного угла [m]\frac{ ∠ BKC}{2}[/m] и косинусом половинного угла [m]\frac{α}{2}[/m]
По условию
tg∠ BKC=2sqrt(2) ⇒ 1+tg^2 ∠ BKC =9
По формулам [i] тригонометрии[/i]
[m]1+tg^2 ∠ BKC =\frac{1}{cos^2∠ BKC}[/m] ⇒ [red][m] cos^2∠ BKC=\frac{1}{9}[/m][/red] ⇒
Так как tg∠ BKC=2sqrt(2) > 0 ⇒ ∠ BKC- острый.
[red][m] cos∠ BKC=\frac{1}{3}[/m][/red]
Синус половинного аргумента:
sin^2 [m]\frac{ ∠ BKC}{2}=\frac{1-cos∠ BKC}{2}=\frac{1-\frac{1}{3}}{2}=\frac{1}{3}[/m]
sin [m]\frac{ ∠ BKC}{2}=\frac{\sqrt{3}}{3}[/m]
Получаем в полученное ранее равенство: sin [m]\frac{ ∠ BKC}{2}=\frac{1}{2cos\frac{α}{2}}[/m]
⇒
[m]\frac{1}{2cos\frac{α}{2}}=\frac{\sqrt{3}}{3}[/m] ⇒[m] cos\frac{α}{2}=\frac{\sqrt{3}}{2}[/m] ⇒
[m]\frac{α}{2}=30 ° [/m] ⇒ [m] α =60 ° [/m]
О т в е т. 60 °
Все решения


