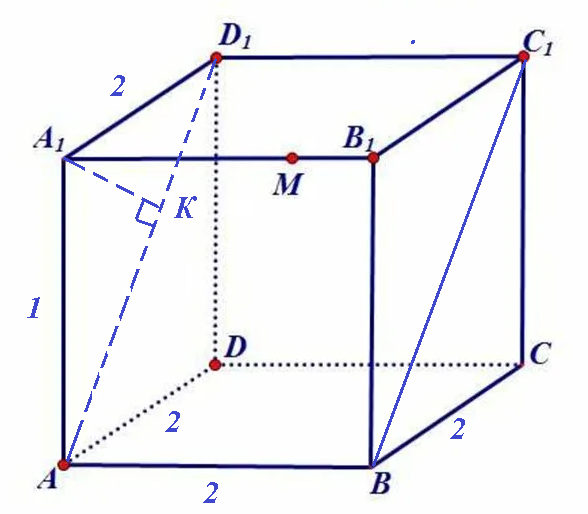
Задача 61780 Для прямоугольного параллелепипеда...

619e48df21b169759d75fdaa

24.11.2021 18:20:02

Для прямоугольного параллелепипеда ABCDA1B1C1D1, у которого AB=2, AD=2, AA1=1, найдите расстояние от вершины A1 до плоскости ABC1

5f3ea7e3faf909182968ddd9

24.11.2021 23:56:41

★

Из прямоугольного треугольника
АА_(1)D_(1)

AD^2_(1)=1^2+2^2=5 ⇒ AD_(1)=[blue]sqrt(5)[/blue]

S_( Δ АА_(1)D_(1))=(1/2) AA_(1)*A_(1)D=(1/2)*1*2=[b]1[/b]

S_( Δ АА_(1)D_(1))=(1/2)AD_(1)*A_(1)K

⇒ =(1/2)AD_(1)*A_(1)K=1

(1/2)*[blue]sqrt(5)[/blue]*A_(1)K=1

A_(1)K=2/sqrt(5)=[red]2sqrt(5)/5[/red]