Задача 63881 Решите задачу по геометрии с правильной...
Условие

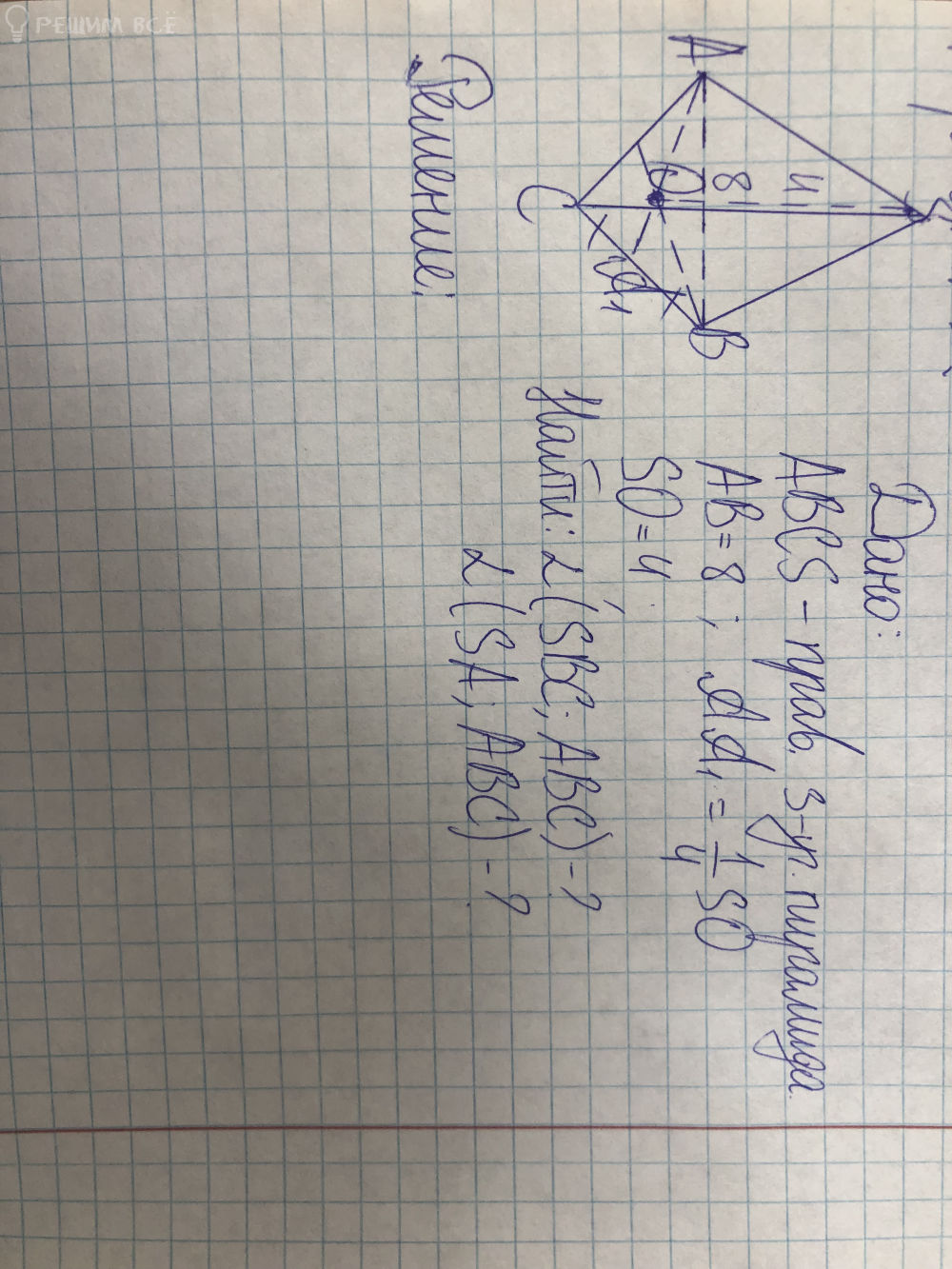
Решение
АВС- равносторонний треугольник.
[b]АВ[/b]=ВС=АС=[b]8[/b]
AA_(1)-медиана, а значит высота и биссектриса.
По теореме Пифагора АА^2_(1)=AB^2+BA^2_(1)
или
AA_(1)=АВ*sin60 ° =8*sqrt(3)/2=4sqrt(3)
Медианы в точке пересечения делятся в отношении 2:1, считая от вершины.
О- точка пересечения медиан и биссектрис и высот равностороннего треугольника
ОА_(1)=(1/3)AA_(1)=4sqrt(3)/3
АО==(2/3)AA_(1)=8sqrt(3)/3
А дальше что то не так
По условию
AA_(1)=(1/4)SO ⇒
SO=4*AA_(1)=16*sqrt(3)
А в условии написано [red]SO=4[/red]
a) ∠ (SBC, ABC)= ∠ SA_(1)O
Из треугольника SA_(1)O
tg ∠ SA_(1)O=SO/OA_(1)
б) ∠ (SA, ABC)= ∠ SAO
Из треугольника SAO
tg∠ SAO=SO/AO