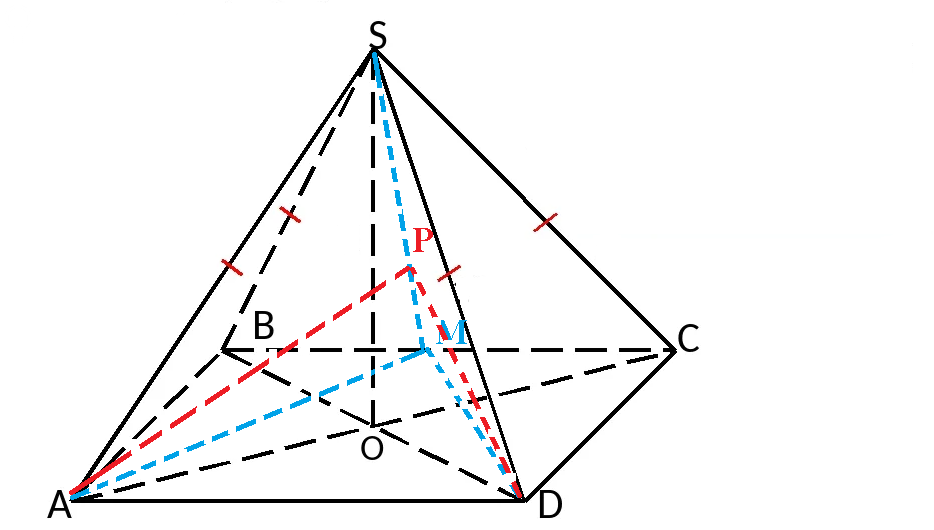
Задача 63119 В основании четыругольной пирамилы SABCD...

62055cd5891e5760b85f34d4

10.02.2022 21:45:01

В основании четыругольной пирамилы SABCD лежит прямоуголньки ABCD. Точка M- серелина реьра BC. Известно, что AD=2AB, а SA= SB= SC= AD. Найдите угол между плоскостями SAM и SDM

5f3ea7e3faf909182968ddd9

13.02.2022 09:31:23

★

Плоскости SAM и SDM пересекаются по прямой [b]SM[/b]

Проводим в каждой плоскости перпендикуляры к линии пересечения [b]SM[/b]

∠ APD - искомый угол.

Его можно найти из Δ APD по теореме косинусов.

Для этого надо найти [b]AP[/b] - высоту Δ SAM

Обозначим

[b]BC=x
[/b]
[b]AD=2x
[/b]
SA= SB= SC= [b]AD=2x[/b]


BD=AC=sqrt(x^2+(2x)^2)=x*sqrt(5)

AO=(1/2)AC=(1/2)*x*sqrt(5)=(x*sqrt(5))/2


SO^2=SA^2-AO^2=(2x)^2-((x*sqrt(5))/2)^2=...

SM^2=SO^2+OM^2=

....

Решайте...