Задача 63588 ...
Условие
6 В кубе A₁...D₁ найдите угол между прямой A₁B и плоскостью ACD₁.
7 В кубе A₁...D₁ найдите угол между прямой AC₁ и плоскостью BB₁D₁.
10 В кубе A₁...D₁ найдите угол между прямой BD₁ и плоскостью BCC₁.
14 В кубе A₁...D₁ найдите угол между прямой AC и плоскостью BCD₁.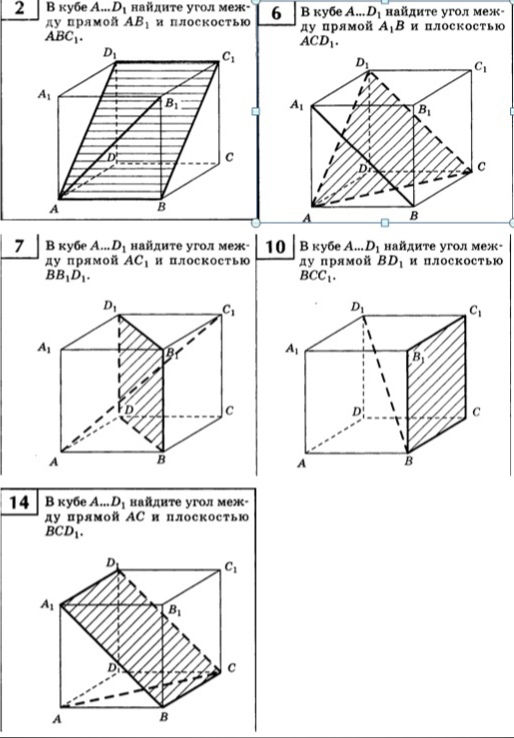
Решение
Угол между прямой и плоскостью - это угол между прямой и ее проекцией на плоскость.
[b]Проводим[/b]
B_(1)K ⊥ BC_(1)
АK- проекция АВ_(1)
АВ_(1)=sqrt(2) ( диагональ квадрата АА_(1)ВВ_(1) со стороной 1)
В_(1)К=sqrt(2)/2 ( половина диагонали квадрата ВВ_(1)С_(1)С)
∠ В_(1)АК=30 ° ( катет против угла в 30 ° равен половине гипотенузы)
6.
A_(1)B || CD_(1)
Значит A_(1)B || пл АCD_(1)
Угол между прямой и плоскостью равен 0
7.
Угол между прямой и плоскостью – угол между прямой и ее проекцией на плоскость.
Проводим A1C1 ⊥ B1D1
и АС ⊥ BD
Проекцией АС1 является MK
Угол АОК – искомый, находим из треугольника AOK
tg ∠ AOK=AK/OK=√2/2/1/2= √2
АК=AC/2=√2/2
ОК=(1/2)МК=1/2
О т в е т. ∠ AOK= arctg(√2)
10.
Угол между прямой и плоскостью – угол между прямой и ее проекцией на плоскость.
Проекцией BD1 является BС1.
Угол C1BD1 – искомый, находим из треугольника C1BD1
tg ∠ C1BD1=C1D1/BC1=1/√2=√2/2
∠ C1BD1=arctg (√2/2)
О т в е т. ∠ C1BD1=arctg (√2/2)
14.
Угол между прямой и плоскостью – угол между прямой и ее проекцией на плоскость.
[b]Проводим[/b]
AK ⊥ A_(1) B
CK- проекция АC
АC=sqrt(2) ( диагональ квадрата АBCD со стороной 1)
AК=sqrt(2)/2 ( половина диагонали квадрата АА_(1)ВВ_(1))
∠ АCК=30 ° ( катет против угла в 30 ° равен половине гипотенузы)